Топологические методы анализа надежности
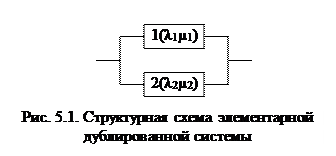
Топологическими называют методы определения показателей надежности либо по графу состояний, либо по структурной схеме надежности. Этими методами, не прибегая к математическому моделированию технической системы, можно вычислить различные показатели надежности: вероятность безотказной работы при заданной наработке, среднюю наработку до отказа или на отказ, функцию и коэффициент готовности системы. К достоинствам топологических методов относят: наглядность, простоту вычислений, допустимость приближенных оценок, возможность анализа надежности разнообразных систем (с восстановлением и без, с резервированием и без) при любой структурной схеме. Применение этих методов значительно усложняется в системах с переменными потоками отказов и восстановлений и в сложных системах, описываемых многосвязными графами состояний. Топологический анализ надежности систем по графу состояний основан на том, что граф состояний полностью описывает все состояния системы и все переходы из одного состояния в другое. Граф состояний системы может быть представлен в матричной форме – в виде матрицы состояний и матрицы переходов. Матрицы состояний и переходов. Совокупность всех состояний системы Е содержит в себе два класса множеств: Е+ – множество работоспособных состояний, Е- – множество неработоспособных состояний. В каждый момент времени t и для каждого состояния k может существовать несколько подмножеств множества всех элементов системы. Для систем с восстановлением элементов таких подмножеств шесть: · Rk – работающие элементы; · Wk – ремонтируемые; · R'k – простаивающие в результате прерывания функционирования; · W'k – простаивающие в результате прерывания восстановления; · R 0 k – находящиеся в очереди на включение в работу; · W 0 k – находящиеся в очереди на восстановление. Каждому k -му состоянию из множества Е соответствует вектор Ak = (a 1 k , a 2 k ,..., amk), характеризующий состояние всех элементов системы в момент времени t. Компоненты aik вектора равны: · si, если i -й элемент принадлежит подмножеству Rk или R'k; · τ i, если i -й элемент принадлежит подмножеству Wk или W'k; · 0, если i -й элемент принадлежит подмножеству R 0 k или W 0 k. При aik = 0 компонента называется нулевой. Функционирование любой восстанавливаемой системы полностью характеризуется матрицей состояний S размерностью m ´ n (m – число элементов, n – число состояний системы, равное числу вершин графа), столбы которой образуют векторы Ak. Для наглядности матрица состояний дополняется верхней строкой, содержащей соответствующие столбцам коды (или номера) состояний, и нижней строкой, в которой цифрой «1» обозначены работоспособные состояния системы, а «0» – неработоспособные. Ветви графа состояний представляют собой графическое изображение всех возможных переходов системы, причем, каждый элементарный переход (шаг) соответствует одному отказу или одному восстановлению элемента. Все возможные переходы за один шаг содержит матрица переходов P. Ее размерность совпадает с размерностью матрицы состояний. Правила построения матрицы переходов таковы: столбцы матрицы соответствуют кодам (или номерам) состояний системы, строки – номерам элементов системы, в каждой ячейке матрицы на пересечении k -го состояния и i -го элемента проставляется код того состояния, в которое попадает система из k -го состояния вследствие отказа (восстановления) i -го элемента. Если такой переход невозможен или отсутствует в графе состояний, то соответствующая ячейка матрицы переходов не заполняется или в ней ставится прочерк. Рассмотрим построение матриц состояний и переходов на простой системе с дублированием и восстановлением элементов (рис. 5.1). Граф состояний этой системы зависит от описания реализуемых состояний.
Цифрой «0» обозначим состояние исправной работы обоих элементов (код состояния – 11). Цифрой «1» – состояние отказа и нахождения в ремонте элемента 1 и исправной работы элемента 2 (код состояния – 01). Цифрой «2» – состояние отказа и нахождения в ремонте элемента 2 и исправной работы элемента 1 (код состояния – 10). Цифрой «3» – состояние отказа системы, когда оба элемента неисправны и оба находятся в ремонте. В этом случае граф состояний выглядит так, как показано на рис. 5.2.
Матрица состояний системы S
Матрица переходов P
Если каждому состоянию системы (столбцу матрицы состояний) сопоставить функцию, аргументами которой служат компоненты соответствующего столбца плюс время, то эта функция есть плотность распределения вероятности пребывания системы в данном состоянии в данный момент времени Преобразование Лапласа. В теории надежности вероятности событий и состояний описывают дифференциальными, интегральными или смешанными линейными уравнениями. Число дифференциальных уравнений системы равно числу узлов графа состояний. Применяя к дифференциальным уравнениям преобразование Лапласа, можно получить более простые для решения алгебраические уравнения, а затем по найденным изображениям восстановить искомые функции – оригиналы или их моменты: математическое ожидание, дисперсию и др. Преобразование Лапласа L [ f (t)]заключается в том, что функции действительной переменной t – оригиналу f (t) ставится в соответствие функция комплексной переменной z – изображение φ(z):
Функция-оригинал восстанавливается по функции-изображению с применением формулы обращения:
где интеграл берется по прямой Rez=c. Некоторые преобразования Лапласа, использующиеся в теории надежности, приведены в табл. 5.1. Таблица 5.1
|


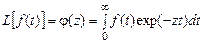 . (5.1)
. (5.1) , (5.2)
, (5.2)


