Теоретические сведения. В ПЗ 2 приведены основные соотношения для расчета показателей безотказности систем при различных видах резервирования
В ПЗ 2 приведены основные соотношения для расчета показателей безотказности систем при различных видах резервирования. В данной работе рассматривается система с общим резервированием, в которой в каждый период работы системы длительностью τ, элемент работает не непрерывно, а на отрезке времени [a;b], длительность которого меньше периода τ. Выключение и включение элемента происходят мгновенно и без влияния на надежность элемента. Если вероятность безотказной работы элемента, работающего без прерывания, равна P(t), то при наличии отрезков прерывания она равна: Pпр(t)=1 при 0<t≤a Pпр(t)=P(t-k(τ-b+a)-a) при kτ+a<t≤kτ+b; k=0,1,2,…. (6.1) Pпр(t)=P(k(b-a)) при (k-1)τ+b<t≤kτ+a; k=1,2,….. Среднее время наработки до отказа равно: а при наличия прерывания в работе элемента:
При экспоненциальном законе распределения:
Выигрыш в наработке до отказа элемента, работающего с прерыванием, равен:
В резервированной системе с одним основным и (n-1) резервными элементами равной надежности вероятность безотказной работы системы равна:
Средняя наработка до отказа системы при экспоненциальном законе распределения:
Выигрыш в наработке до отказа системы с резервированием равен: Из сравнения выражения (6.4) видно, что режим с прерыванием работы может дать заметный выигрыш в показателях безотказности. Рассмотрим это на примере простой системы с общим резервированием/дублированием по рис. 6.1. Все элементы равнонадежны, закон распределения – экспоненциальный, интенсивность отказов l=0,002 1/час, режимы работы элементов за период работы системы τ= 10 час следующие: 1[0;5], 2[2;4], 3[5;10], 4[0;6].
Результаты расчетов вероятности безотказной работы системы с непрерывной (Рс) и прерывистой (Рспр) работой элементов приведены на рис. 6.2..
Расчетные значения наработок до отказа элементов равны Т1пр≈1000 час, Т2пр≈2500 час, Т3пр≈1005 час, Т4пр≈833 час (при Тэл=1/l=500 час). Таким образом, наработка до отказа элемента, работающего с прерыванием, возрастает примерно пропорционально отношению τ/(b-a). Средняя наработка до отказа системы также возрастает. Приблизительно ее можно оценить по соотношению Тспр ≈ max(min(Т1пр;Т2пр);min(Т3пр;Т4пр)) ≈ 1000 час. Рассчитать Тспр можно по кривой изменения вероятности безотказной работы от наработки. При экспоненциальном законе распределения Рспр(Тспр)=1/е =1/2,718, откуда находим Тспр≈980 час. Выигрыш от резервирования системы равен Примечание: В рассмотренном примере длительности прерывания работы элементов заданы произвольно. Поэтому при совокупной работе всех элементов по принятому графику система за один цикл, равный τ=10 час, находится в работоспособном состоянии всего три часа – когда одновременно работают элементы 1 и 2 или 3 и 4, что соответствует ФАЛ работоспособного состояния системы: А=а1Ùа2˅а3Ùа4. Из этого можно предположить, что существенное увеличение наработки до отказа главным образом связано с работой системы не на всем протяжении цикла, т.е. с прерыванием, как и все ее элементы. Чтобы исключить влияние этого фактора в вариантах расчетных заданий интервалы работы элементов системы в пределах цикла подобраны так, чтобы система работала без прерывания в течение цикла τ.
|

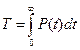 ,
, (6.2)
(6.2)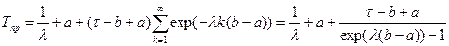 . (6.3)
. (6.3) . (6.4)
. (6.4)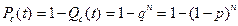 .
.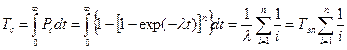 .
. .
.

 ≈ 980/375 ≈ 2,6.
≈ 980/375 ≈ 2,6.


