Определение риска системы по точной формуле
Риск системы вычисляется по формуле 7.3. 1.Сформировать вектор { λiri }, состоящий из скалярного произведения векторов { λi } и { ri }. Для ускорения процедуры ввода значения λ; не умножаются на 10-5. В результате получится вектор:
2.Для нахождения суммы значений вектора воспользоваться стандартной функцией СУММ:
3.Вероятность отказа Qc рассчитать по формуле: Qc(t)=1-Pc(t) при λс =9,2·10-5. Тогда в общем виде функция риска системы равна:
Вычисление Rc(t) для заданного времени непрерывной работы t = T и среднего времени безотказной работы t = T1 проводятся подстановкой значений T и T1 в формулу. Для t = T =1500 час Rс (1500)= 2568,15·(1-exp(-9,2·0,00001·1500))= 331,04. Для t = T1 =10870 час Rс (1500)= 2568,15·(1-exp(-9,2·0,00001·10870))= 1623,42. Из полученных значений Rc(t) видно, что риск исследуемой системы ниже допустимого значения, равного 8000 условных единиц.
Определение критического времени работы системы Так как Rc(t) возрастает с увеличением t, то целесообразно определить время τ;, при достижении которого риск превысит допустимое значение. Решение задачи сводится к определению корня уравнения 7.3. В нашем случае λс =9,2·10-5 час-1, R =8000 и Решая это уравнение, находят критическое значение τ. В нашем примере вещественного корня нет. Это значит, что при любом t риск системы не превысит допустимого значения.
|
.
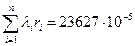. Подставляя эти значения в уравнение 6.3, получим: 8000=2568[1-exp(-9,210-5 τ;)].
