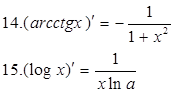Лекция №6
Тема: Производная и дифференциал функции Производные основных элементарных функций. План:
Ключевые слова: производная функции, дифференциал, приращение функции, формула Лейбница. Производной функции
Если функция в точке Функция дифференцируемая в каждой точке промежутка Геометрический смысл производной: производная Тогда уравнение касательной к кривой
Механический смысл производной: производная пути по времени Теорема. Если функция Производная функции 1.Дадим аргументу 2.Находим приращение функции 3.Составляем отношение 4.Находим предел этого отношения при Правила дифференцирования 1. Производная постоянной равна нулю, то есть 2. Производная аргумента равна 1, то есть 3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть
5. Производная частного двух дифференцируемых функций может быть найдена по формуле:
Теорема. Если
Теорема. Для дифференцируемой функции с производной не равной нулю, производная обратной функции равна обратной величине производной данной функции, то есть Таблица производных
|

 называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует)
называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует) .
.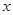 имеет конечную производную, то функция называется дифференцируемой в этой точке.
имеет конечную производную, то функция называется дифференцируемой в этой точке. , называется дифференцируемой на этом промежутке.
, называется дифференцируемой на этом промежутке. есть угловой коэффициент (тангенс угла наклона) касательной, приведенной к кривой
есть угловой коэффициент (тангенс угла наклона) касательной, приведенной к кривой  .
. .
. есть скорость точки в момент времени
есть скорость точки в момент времени  :
: 
 и найдем наращенное значение функции
и найдем наращенное значение функции  .
. .
.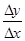 .
. , то есть
, то есть  (если этот предел существует).
(если этот предел существует). .
. .
.

 .
. и
и  - дифференцируемые функции от своих переменных, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной
- дифференцируемые функции от своих переменных, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной  .
.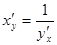 .
.