План:
- Определенный интеграл по Риману.
- Нижняя и верхняя интегральные суммы Дарбу.
Ключевые слова: интегральная сумма, суммы Дарбу, нижняя и верхняя суммы.
Пусть на отрезке  задана функция
задана функция  . Разобьем отрезок
. Разобьем отрезок  на
на  элементарных отрезков точками
элементарных отрезков точками 
 .
.
Точки, разделяющие отрезок [ а, b ] на частичные отрезки  длиной
длиной 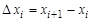 , называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку
, называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку  . Образуем сумму произведений
. Образуем сумму произведений
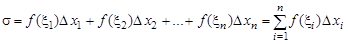 ,
,
На каждом отрезке  разбиения выберем некоторую точку
разбиения выберем некоторую точку  и положим
и положим  , где
, где  . Сумму вида
. Сумму вида
 (1)
(1)
будем называть интегральной суммой для функции  .на
.на  . Для избранного разбиения отрезка
. Для избранного разбиения отрезка  на части обозначим через
на части обозначим через  максимальную из длин отрезков
максимальную из длин отрезков  , где
, где  .
.
Пусть предел интегральной суммы при стремлении  к нулю существует, конечен и не зависит от способа выбора точек
к нулю существует, конечен и не зависит от способа выбора точек  и точек
и точек  . Тогда этот предел называется определенным интегралом от функции
. Тогда этот предел называется определенным интегралом от функции  на
на  , обозначается
, обозначается  , а сама функция
, а сама функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке  , то есть
, то есть
 =
= 
 .
.
называемую интегральной суммой для функции  на отрезке [ а, b ]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями
на отрезке [ а, b ]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями  и высотами
и высотами  .
.
При этом числа a и b называются соответственно нижним и верхним пределами, выражение 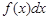 – подынтегральным выражением,
– подынтегральным выражением,  – подынтегральной функцией.
– подынтегральной функцией.
Определенный интеграл численно равен площади криволинейной трапеции, ограниченной вертикальными прямыми  при
при  , осью Ох и графиком неотрицательной и непрерывной функции
, осью Ох и графиком неотрицательной и непрерывной функции  . В этом состоит его геометрический смысл.
. В этом состоит его геометрический смысл.
Экономический смысл интеграла. Если  - производительность труда в момент времени
- производительность труда в момент времени  , то
, то  есть объем выпускаемой продукции за промежуток
есть объем выпускаемой продукции за промежуток
 . Величина и объем продукции, произведенной за промежуток времени
. Величина и объем продукции, произведенной за промежуток времени  , численно равна площади под графиком функции
, численно равна площади под графиком функции  , описывающей изменение производительности труда с течением времени, на промежутке
, описывающей изменение производительности труда с течением времени, на промежутке  или
или  .
.

 задана функция
задана функция  . Разобьем отрезок
. Разобьем отрезок  элементарных отрезков точками
элементарных отрезков точками 
 .
. длиной
длиной 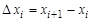 , называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку
, называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку  . Образуем сумму произведений
. Образуем сумму произведений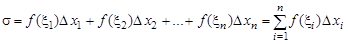 ,
, разбиения выберем некоторую точку
разбиения выберем некоторую точку  и положим
и положим  , где
, где  . Сумму вида
. Сумму вида (1)
(1) максимальную из длин отрезков
максимальную из длин отрезков  к нулю существует, конечен и не зависит от способа выбора точек
к нулю существует, конечен и не зависит от способа выбора точек  и точек
и точек  . Тогда этот предел называется определенным интегралом от функции
. Тогда этот предел называется определенным интегралом от функции  , а сама функция
, а сама функция 
 на отрезке [ а, b ]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями
на отрезке [ а, b ]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями  и высотами
и высотами  .
.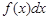 – подынтегральным выражением,
– подынтегральным выражением,  при
при  , осью Ох и графиком неотрицательной и непрерывной функции
, осью Ох и графиком неотрицательной и непрерывной функции  . В этом состоит его геометрический смысл.
. В этом состоит его геометрический смысл. - производительность труда в момент времени
- производительность труда в момент времени  , то
, то  есть объем выпускаемой продукции за промежуток
есть объем выпускаемой продукции за промежуток . Величина и объем продукции, произведенной за промежуток времени
. Величина и объем продукции, произведенной за промежуток времени  , описывающей изменение производительности труда с течением времени, на промежутке
, описывающей изменение производительности труда с течением времени, на промежутке 


