Лекция №7
Тема Неопределенный интеграл. План: 1. Понятие первообразной функции. 2. Неопределенный интеграл. 3. Основные свойства неопределенного интеграла. 4. Интегрирование заменой переменой. 5. Интегрирование по частям
Ключевые слова: первообразная функции, интегрирование, замена переменной и интегрирование по частям.
Функция Теорема. Если
Множество всех первообразных для функции Свойства неопределенного интеграла 1.Производная от неопределенного интеграла равна подынтегральной функции, то есть
2.Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
3.Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, то есть
где 4.Постоянный множитель можно выносить за знак интеграла, то есть
5.Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, то есть
Метод замены переменной
где
Метод интегрирования по частям
где 1. 3. 5. 7. 9. 11.
|

 называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке  , если в любой точке этого промежутка
, если в любой точке этого промежутка  .
. и
и  - первообразные для функции
- первообразные для функции  , что будет справедливо равенство
, что будет справедливо равенство . Таким образом,
. Таким образом,  .
.
 ,
,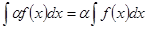
 .
. ,
, - функция, дифференцируемая на рассматриваемом промежутке.
- функция, дифференцируемая на рассматриваемом промежутке. ,
, и
и  - дифференцируемые функции.
- дифференцируемые функции.
 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 



