Лекция №3
Тема:Элементы векторной алгебры и матричного анализа. План 1. Векторы на плоскости и в пространстве; 2. скалярное произведение векторов; 3. линейно зависимые и линейно независимые системы векторов ключевые слова: Векторы на плоскости и в пространстве; скалярное произведение векторов; линейно зависимые и линейно независимые системы векторов.
Векторы b, c, d, e, f – компланарны, а вектор а c любыми двумя некомпланарны. Коллинеарными называются вектора лежащие на одной прямой. Компланарными называются вектора лежащие в одной плоскости. Вектор - направленный отрезок – упорядоченная пара точек P и Q пространства, где P – начало направленного отрезка – точка приложения вектора, а Q – его конец(обозначение PQ). Вектор, начало и конец которого совпадают называется нулевым. Направление нулевого вектора не определено. Расстояние между точками A и B называют длинной или модулем вектора(|AB|). Определение(равенство векторов AB=CD): A=B и C=D (т.е. AB и CD нулевые векторы) векторы не единичны, лежат на одной прямой, имеют одинаковую длину и направление.
Если AB=CD, то CD=AB. Если AB=CD и CD=EF, тогда AB=EF. Если AB=CD, то |AB|=|CD|. Для любых трех точек A, B и C существует единственная точка D такая, что: AB=CD. Линейные операции над векторами: A) Сложение векторов: Теорема(свойства сложения векторов): для любых двух векторов u и v существует единственный вектор u+v, называемый их суммой. u + v=v + u (коммутативно) (u + v) + w = u + (v + w) (ассоциативно) существует единственный вектор 0, называемый нулевым вектором, такой, что 0 + u = u Существует единственный вектор –u, такой, что u + (-u) = 0 B) Умножение вектора на число: Пусть u – свободный вектор, а a – число, тогда au – свободный вектор, порожденный вектором u. (au=-(-a)u) Теорема(умножение вектора на число) Для любого вектора u и любого числа a существует единственный вектор au. (a1 + a2)u=a1u + a2u a1a2u=a1(a2u) a(u1 + u2) = au1 + au2 1*u=u Выражение a1u1+a2u2+…+anun – линейная комбинация векторов. Базис: Базис на прямой – обыкновенный вектор. Базис на плоскости – два неколлинеарных вектора e1, e2, данных в определенном порядке и приложенных к точке О – началу базиса. Базис в пространстве – тройка некомпланарных векторов e1, e2, e3, данных в определенном порядке и приложенных к точке О – началу базиса. Базис называется ортонормированным, если его векторы попарно ортогональны и по величине равны единицы. Теорема: В ортонормированном базисе: Если a=(xa;ya;za), и b=(xb;yb;zb) тогда c=(a;b)=xaxb+yayb+zazb;
|


 A, B, C, D – разные точки, никакие три из них не лежат на одной прямой, AB||CD и AC||BD. Обладают следующими свойствами:
A, B, C, D – разные точки, никакие три из них не лежат на одной прямой, AB||CD и AC||BD. Обладают следующими свойствами: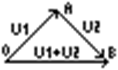 Если u1 и u2 два свободных вектора, то приложим их к какой-нибудь точке O. Получившийся вектор OB называется их суммой, т.е. OB=OA+AB.
Если u1 и u2 два свободных вектора, то приложим их к какой-нибудь точке O. Получившийся вектор OB называется их суммой, т.е. OB=OA+AB.


