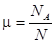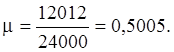Аксиомы теории вероятностей
При аксиоматическом подходе к изложению теории вероятностей за основу берется некоторое множество W, элементы w которого называются элементарными событиями, а само W - пространством элементарных событий. Зафиксируем некоторую непустую систему S, состоящую из подмножества А, В, … пространства элементарных событий. Подмножества А, В,… назовем событиями. Относительно структуры системы S предположим выполненными следующие две аксиомы событий: I. Если множества А1, А2, … (в конечном или счетном числе) являются событиями, то их объединение А1 È А2 È… тоже является событием. II. Если множество А является событием, то его дополнение W \ А до множества W тоже является событием. Система S, удовлетворяющая аксиомам I и II, называется борелевским полем событий. Из аксиом I и II вытекает, что W Î S, Æ Î S и если Ai Î S (i = 1, 2, …), то А1 Ç А2 Ç.. Î S. В дальнейшем операцию объединения событий будем называть сложением и обозначать знаком «+», операцию пересечения – умножением и обозначать знаком «-», а операцию дополнения – переходом к противоположному событию и выделять чертой сверху (например, В новых обозначениях аксиомы I и II запишутся: I. А1, А2,… Î S Þ А1 + А2 + … Î S. II. А Î S Þ События А и В назовем несовместными, если АВ = V (т.е. АÇВ = Æ). Аксиомы вероятностей: 1. Каждому событию А поставлено в соответствие неотрицательное число р(А), называемое вероятностью события А. 2. Если события А1, А2, … попарно несовместны, то р(А1 + А2 + …) = р(А1) + р(А2) + … (аксиома счетной аддитивности) 3. p(U) = 1. Совокупность трех объектов < W, S, p(A) >, в которой S удовлетворяет аксиомам I и II, а функция р(А) – аксиомам 1, 2, 3, назовем вероятностной схемой.
Правило произведения. Пусть элемент х1 строки (х1, х2, …, хk) можно выбрать n1 способами; после каждого выбора х1 элемент х2 можно выбрать n2 способами; после выборов х1 и х2 элемент х3 можно выбрать n3 способами и т.д.; после выборов х1, х2, …, хk-1 элемент хk можно выбрать nk способами. Тогда строку (х1, х2, …, хk) можно образовать n1 × n2 × … × nk способами. Пример 1. Сколькими способами можно выбрать четырехзначное число, все цифры которого различны? Решение. Каждому четырехзначному числу можно поставить во взаимно однозначное соответствие строку (х1, х2, х3, х4), где х1, х2, х3, х4 – соответственно 1, 2, 3 и 4-я цифры. Элемент х1 этой строки можно выбрать 9 способами (любую из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9); элемент х2 можно выбрать также 9 способами (теперь можно использовать и цифру 0, но первую выбранную цифру повторить нельзя); элемент х3 можно выбрать 8 способами (уже выбранные первые две цифры повторить нельзя); наконец, элемент х4 можно выбрать 7 способами. Согласно правилу произведения искомое число способов выбора четырехзначного числа с различными цифрами равно: 9 × 9 × 8 × 7 = 4536. Размещения с повторениями. Пусть Х – множество, состоящее из n элементов (n-членное множество). Тогда любая строка длиной k, составленная из элементов множества Х, называется размещением с повторениями из n элементов по k. Число всех размещений с повторениями из n элементов по k равно nk. Пример 2. Сколькими способами можно выбрать четырехзначное число, в десятичной записи которого нет нуля? Решение. Четырехзначные числа указанного вида можно рассматривать как строки длиной 4, составленные из элементов множества Х = {1, 2, 3, 4, 5, 6, 7, 8, 9}, т.е. как размещения с повторениями из 9 элементов по 4. Следовательно, искомое число способов равно: 94 = 6561. Размещения без повторений. Перестановки. Пусть Х по-прежнему n -членное множество. Тогда любая строка длиной k, составленная из различных элементов множества Х, называется размещением без повторений из n элементов по k. Число всех таких размещений обозначается
В случае, когда k = n, размещения без повторений называются перестановками из n элементов. Число всех перестановок из n элементов обозначается Pn и равно: Pn = Пример 3. 10 спортсменов разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами? Решение. Предположим, что спортсмены пронумерованы числами от 1 до 10 и х1, х2, х3 – номера спортсменов, получивших золотую, серебряную и бронзовую медали. Каждому такому распределению медалей соответствует строка (х1, х2, х3), состоящая из различных чисел (номеров спортсменов). Обратно каждой строке (х1, х2, х3) соответствует способ распределения медалей. Следовательно, число способов распределения медалей равно числу размещений без повторений из 10 элементов по 3, т.е. Сочетания и бином Ньютона. Всякое k -членное подмножество n-членного множества называется сочетанием из n элементов по k. Число различных сочетаний из n элементов по k обозначается
Числа (a + b) n = Пример 4. Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек? Решение. Очевидно, команда из 6 человек является 6-членным подмножеством 10-членного множества, т.е. сочетанием из 10 элементов по 6. Следовательно, искомое число способов равно Размещения данного состава. Полиномиальная формула. Размещением данного состава (k1, k2,…, km) из элементов m -членного множества Х = { x1, x2,…, xm } называется всякая строка длинной k1 + k2 + … + km = n, составленная из элементов множества Х, так, что элемент х1 повторяется k1 раз, элемент x2 – k2 раз и т.д., элемент xm – km раз. Например, если Х= { x1, x2,x3 }, то (x1, x2, x2, х1, х1) есть размещение состава (3,2,0). Количество различных размещений заданного состава (k1, k2,…, km) обозначается А(k1, k2,…, km) и равно:
Следующая формула, обобщающая формулу бинома Ньютона, называется полиномиальной:
где суммирование проводится по всевозможным наборам целых неотрицательных чисел k1, k2,…, km, для которых k1 + k2 + … + km = n. Пример 5. Сколькими способами можно поставить на книжной полке 3 экземпляра учебника по алгебре, 2 экземпляра учебника по геометрии и один экземпляр учебника по математическому анализу? Решение. Очевидно, всякой расстановке указанных учебников взаимно однозначно соответствует строка длиной 3 + 2 + 1 = 6 состава (3, 2,1). Следовательно, искомое число способов равно числу размещений состава (3, 2, 1).т.е.
Пример 6. Вычислите (1 + х + х2)3. Решение. По полиномиальной формуле имеем:
где суммирование производится по всем наборам неотрицательных целых чисел k1, k2, k3, для которых k1 + k2 + k3 = 3. Выпишем все такие наборы: (0,0,3), (0,3,0), (3,0,0), (0,1,2), (1,2,0), (2,0,1), (1,0,2), (0,2,1), (2,1,0), (1,1,1). Теперь находим:
Пусть А – случайное событие по отношению к некоторому испытанию. Представим себе, что это испытание произведено N раз и при этом событие А наступило в NA случаях. Тогда отношение
называется частотой события А в данной серии испытаний. Определение. Вероятностью случайного события А называется число р(А), около которого колеблется частота этого события в длинных сериях испытаний.
Пример 1. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Частота рождения мальчика в такой серии наблюдений равна 0,515. Пример 2. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз, и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения герба в данной серии испытаний равна:
Пример 3. Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз, причем герб выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:
Примеры 2 и 3 подтверждают естественное предположение о том, что вероятность выпадения герба при одном бросании монеты равна 0,5.
|

 ). Кроме того, событие W назовем достоверным и обозначим U, Æ - невозможным и обозначим V.
). Кроме того, событие W назовем достоверным и обозначим U, Æ - невозможным и обозначим V. .
. и равно:
и равно: .
. = n!.
= n!.
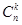 . Справедлива формула
. Справедлива формула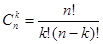 .
.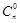 ,
,  ,
,  ,…,
,…, 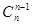 ,
,  являются коэффициентами в разложении бинома Ньютона:
являются коэффициентами в разложении бинома Ньютона: a0 bn +
a0 bn +  a bn-1 + … +
a bn-1 + … + 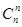 an b0.
an b0.
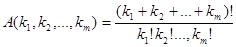 .
. ,
,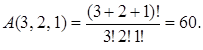
 ,
,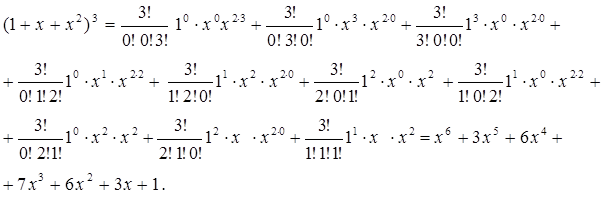 2.
2.