Тема: Законы распределение случайных величин. Биноминальный закон распределения. Закон распределения Пуассона. Числовые характеристики.
Реальное содержание понятия «случайная величина» может быть выражено с помощью такого определения: случайной величиной, связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величины будем обозначать жирными буквами х, у,…. Определение. Говорят, что задана дискретная случайная величина х, если указано конечное или счетное множество чисел х1, х2 … и каждому из этих чисел xi поставлено в соответствие некоторое положительное число pi, причем р1 + р2 + …= 1. Числа х1, х2 … называются возможными значениями случайной величины х, а числа р1, р2 ,… - вероятностями этих значений (pi = Р ( х = xi)). Таблица
называется законом распределения дискретной случайной величины х. Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки (xi, pi) и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины х.
Пример 1. По мишени производится 4 независимых выстрела с вероятностью попадания при каждом выстреле р = 0,8. Требуется: а) найти закон распределения дискретной случайной величины х, равной числу попаданий в мишень; б) найти вероятности событий: 1 £ х £ 3; х > 3; в) построить многоугольник распределения. Решение. а) Возможные значения случайной величины х: 0, 1, 2, 3, 4. Соответствующие вероятности вычисляем по формуле Бернулли:
Закон распределения х представится таблицей:
Проверка: 0,0016 + 0,0256 + 0,1536 + 0,4096 + 0,4096 = 1. б) Вероятность событий 1 £ х £ 3 и х > 3 равны: р (1 £ х £ 3) = р ({1,2,3}) = р1 + р2 + р3 = 0,0256 + 0,1536 + 0,4096 = 0,5888; р(х > 3) = р ({4}) = р4 = 0,4096. в) Многоугольник распределения представлен на рисунке 11. Если возможными значениями дискретной случайной величины х являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:
то говорят, что случайная величина х имеет биномиальный закон распределения:
Рассмотренная выше в примере 1 случайная величина х имеет биномиальный закон распределения, в котором n = 4, p = 0,8. Пример 2. В урне 7 шаров, из которых 4 белых, а остальные черные. Из этой урны наудачу извлекаются 3 шара; х – число извлеченных белых шаров. Найдите закон распределения дискретной случайной величины х и вероятность события х ³ 2. Решение. Возможные значения случайной величины х: 0, 1, 2, 3. Соответствующие им вероятности р0, р1, р2, р3 подсчитываем классическим способом:
Закон распределения х:
Вероятность события х ³ 2 равна: р (х ³ 2) = Пусть заданы натуральные числа m, n, s, причем m£ s £ n. Если возможными значениями дискретной случайной величины х являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле pk = p( x = k) = то говорят, что случайная величина х имеет гипергеометрический закон распределения. Случайная величина х из примера 2 имеет гипергеометрический закон распределения с n =7, s = 3, m = 4. Другими часто встречающимися примерами законов распределения дискретной случайной величины являются: геометрический
где pk = qk-1p, q = 1 – p (0 < p < 1); Закон распределения Пуассона:
Закон распределения Пуассона является предельным для биномиального при n ® ¥, p ® 0, np = l = const. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
|


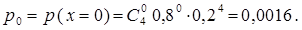
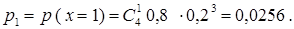



 , k = 0,1,…n; q = 1- p,
, k = 0,1,…n; q = 1- p, ;
;  ;
; ;
; 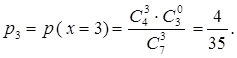




 .
. , k = 0,1,…,m,
, k = 0,1,…,m, , l - положительное постоянное.
, l - положительное постоянное.


