Тема: Статистическая оценка параметров распределения. Несмещенные, эффективные и состоятельные оценки. Точечные оценки.
Пусть Q - неизвестный параметр (математическое ожидание, дисперсия и т.д.) изучаемой случайной величины х и х1, х2,…,хn (1) выборка, полученная в результате n независимых опытов. Члены выборки xi являются случайными величинами в том смысле, что если выполнить новую серию n опытов, то, вообще говоря, получится другие числа: х1', х2',…,хn'. Однако, каждая случайная величина xi имеет такой же закон распределения, что и исходная величина х. Оценкой параметра Q - по данной выборке (1) называется число По отношению к Q назовем Если M [ Если Если m - неизвестное математическое ожидание случайной величины х, то в качестве оценки m применяется выборочное среднее
Выборочное среднее В качестве оценки неизвестной дисперсии D случайной величины х применяется выборочная дисперсия
Выборочная дисперсия
При малом объеме выборки (n £ 30) пользуются исправленной выборочной дисперсией Для выборочной дисперсии справедлива формула
то
Если изучаемая случайная величина непрерывная с интервальной таблицей частот:
то для применения формул (6), (7) и (8) в качестве a i обычно берут середину интервала [ ci, ci+1 [.
|

 (х1, х2,…,хn), зависящее от х1, х2,…,хn и приближенно равноеQ, т.е.
(х1, х2,…,хn), зависящее от х1, х2,…,хn и приближенно равноеQ, т.е.  .
. выборочным параметром величины х. Выборочный параметр
выборочным параметром величины х. Выборочный параметр  также является случайной величиной, так как он будет меняться от одной серии опытов к другой.
также является случайной величиной, так как он будет меняться от одной серии опытов к другой. , то
, то  D [
D [  , равное
, равное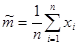 . (2)
. (2) . (3)
. (3) является состоятельной, но смещенной оценкой дисперсии D. Несмещенной и состоятельной оценкой D является исправленная выборочная дисперсия
является состоятельной, но смещенной оценкой дисперсии D. Несмещенной и состоятельной оценкой D является исправленная выборочная дисперсия . (4)
. (4) ; при больших n (n > 30) практически безразлично, какой из двух оценок (
; при больших n (n > 30) практически безразлично, какой из двух оценок ( или
или  . (5)
. (5)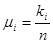
 , (6)
, (6) , (7)
, (7) . (8)
. (8)