Тема: Элементы корреляционно-регрессионного анализа. Дисперсионный анализ. Метод наименьших квадратов.
При изучении связи между случайными величинами х и у важную роль играет коэффициент корреляции r [ x, y ], определяемый формулой
Учитывая, что k[x, y] = M[x y] – M[x] M[y] (см. § 18), можно записать:
Свойства коэффициента корреляции: 1. Если х и у независимы, то r [ x, y ] = 0. 2. Для любых х и у имеет место неравенство ½ r [ x, y ] ½ £ 1. 3. ½ r [ x, y ] ½ = 1 тогда и только тогда, когда между х и у имеется линейная зависимость у = ах + b; причем r [ x, y ] = 1, если a > 0 и r [ x, y ] = -1, если a < 0 (и наоборот).
Система случайных величин (х, у) задана таблицей распределения:
Найдите коэффициент корреляции между х и у. Решение. Воспользуемся формулой (1):
В данном случае M[xy] = 0 × (-1) × 0,10 + 0 × 0 × 0,15 + 0 ×1 × 0,20 + 1 × (-1) × 0,15 + 1 × 0 × 0,25 + + 1 × 1 × 0,15 = 0. Для нахождения M[x], M[y], s [x] и s [x] составим законы распределения величин х и у в отдельности:
Отсюда M[x] = 0 × 0,45 + 1× 0,55 = 0,55; M[y] = (-1) × 0,25 + 0 × 0,040 + 1 × 0,25 = 0,1; D[x] = M[x2] – M[x]2 = 0,55 – 0,552 = 0,2475; s [x] = D[y] = M[y2] – M[y]2 = 0,6 – 0,12 = 0,59; s [y] =
Пример 2. Известно, что M[x] = 5; M[y] = 0,2; D[x] = 4; D[y] = 2,25; r [x,y] = -0,5. Найдите M[xy]. Решение. Из формулы (1) находим: M[xy] = M[x] M[y] + s[x] s[y] r[x,y] = 5 × 0,2 ×
Пусть коэффициент корреляции между величинами х и у неизвестен, но мы располагаем n точками: (х1, у1), (х2 у2),..., (xn yn), (2) полученными в результате n независимых опытов над системой (х, у). Тогда в качестве приближенного значения неизвестного r[ x,y ] берется выборочный коэффициент корреляции:
Пример 3. В результате 10 независимых опытов над системой (х,у) получены точки: (2,1; 3,0), (2,1; 2,8), (2,0; 3,0), (2,5; 2,0), (2,8; 1,8), (2,2; 2,5), (3,2; 1,5), (3,2; 1,1), (3,2; 1,0), (4,7; 1,3). Найдите выборочный коэффициент корреляции. Решение. Для удобства вычислений составляем расчетную таблицу:
Далее находим:
Так как модуль коэффициента корреляции близок к 1, то зависимость между х и у можно считать близкой к линейной, причем корреляция отрицательная (с возрастанием х величина у в среднем убывает). Пусть зависимость у от х близка к линейной и имеется выборка (2). Требуется найти прямую у = ах + b, которая наилучшим образом выражает зависимость у от х. Эта задача решается методом наименьших квадратов (см. [6], § 46). Искомое уравнение имеет вид:
Уравнение (3) называется выборочным уравнением регрессии у на х. Аналогично определяется выборочное уравнение регрессии х на у:
|

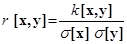 .
. , (1)
, (1) у
х
у
х
 » 0,497;
» 0,497; » 0,768;
» 0,768; .
. ×
×  (-0,5) = -1,5.
(-0,5) = -1,5. .
.

 ;
;  ;
;  ;
; ;
;  ;
;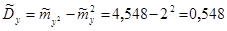 ;
;  ;
; .
. . (3)
. (3) .
.


