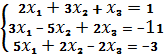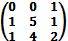Материал для самоконтроля по СРС
Контрольная работа Вариант № 1
1.Найти косинус угла между векторами AB и АС А(2, –2, 3), В(1, – 1, 2), С(4, –4, 5)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
3.Решить систему уравнений по правилу Крамера
4.Найти матрицу С–1, обратную матрице С=
5.Написать разложение вектора
Вариант № 2
1.Найти косинус угла между векторами AB и АС А(0, –2, 6), В(–12, – 2, –3), С(–9, –2, –6)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
3.Решить систему уравнений по правилу Крамера
4.Найти матрицу С–1, обратную матрице С=
5.Написать разложение вектора
Вариант № 3
1.Найти косинус угла между векторами AB и АС А(2, 3, –1), В(4, 5, –2), С(3, 1, 1)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
3.Решить систему уравнений по правилу Крамера
4.Найти матрицу С–1, обратную матрице С=
5.Написать разложение вектора
Вариант № 4
1.Найти косинус угла между векторами AB и АС А(1, 2, –2), В(3, 4, –5), С(1, 1, 0)
2.Написать каноническое уравнение прямой, заданной как линия пересечения двух плоскостей
3.Решить систему уравнений по правилу Крамера
4.Найти матрицу С–1, обратную матрице С=
Написать разложение вектора
|



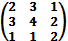
 по векторам
по векторам  ,
, 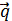 ,
,