Классический способ подсчета вероятностей
Пусть W - конечное пространство элементарных событий А1, А2, …, Аn. В качестве борелевского поля событий рассмотрим систему S всех подмножеств множества W. Ясно, что при этом аксиомы I и II выполняются. При классическом способе подсчета вероятностей все элементарные события считаются равновероятными. И так как р(А1 + А2 +… + Аn) = р(U) = 1, то р(А1) = р(А2) = … = р(Аn) = Если теперь А – произвольное событие и А = Ai1 + …+ Aim, то согласно аксиоме 2 имеем р(А) = События А1, А2, …, Аn принято называть элементарными исходами данного испытания, а те элементарные исходы, которые в сумме составляют событие А, называются благоприятными случаями для А. Количество благоприятных случаев для события А обозначим m(A). Таким образом, р(А) = Пример 1. В урне 10 шаров, из которых 3 белых и 7 черных. Какова вероятность того, что наудачу извлеченный шар из этой урны окажется белым? Решение. Пусть событие А – извлеченный шар оказывается белым. Данное испытание имеет 10 равновероятных исходов, из которых для события А благоприятны три. Следовательно, р(А) = Пример 2. Все натуральные числа от 1 до 20 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны наудачу взята одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5 – событие А; кратным 3 – событие В; простым – событие С; составным – событие D; не простым и не составным – событие Е? Решение. Испытание имеет 20 равновероятных исходов. Из них m(A) = 4; m(B) = 6; m(C) = 8; m(D) = 11; m(E) = 1. Соответственно событиям получим следующие вероятности: p(A) = 0,2; p(B) = 0,3; p(C) = 0,4; p(D) = 0,55; p(E) = 0,05.
Пусть событие А может наступить только с одним из n попарно несовместных событий Н1, Н2, …, Нn, которые по отношению к А называются гипотезами. Тогда вероятность события А можно вычислить по формуле полной вероятности:
Если стало известно, что событие А произошло, то вероятность р (Hi)(i = 1,2,…,n)можно переоценить, т.е. найти условные вероятности p (Hi / A). Эта задача решается по формуле Байеса:
где р (А) вычисляется по формуле полной вероятности. Пример. В первой урне 2 белых и 6 черных шаров, во второй – 4 белых и 2 черных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали один шар. а) Какова вероятность того, что этот шар белый? б) Шар, взятый из второй урны, оказался белым. Какова вероятность того, что из первой урны во вторую были переложены 2 белых шара? Решение. а) Введем обозначения: А – шар, извлеченный из второй урны, белый; гипотезы Н1 – из первой урны во вторую переложены 2 белых шара, Н2 – переложены 2 разноцветных шара, Н3 – переложены 2 черных шара. Тогда р(Н) = р(Нi) p(A/Hi) + p(H2) p(A/H2) + p(H3) p (A/H3). Вероятности гипотез Нi и условие вероятности p(A/ Нi) (i = 1, 2, 3) вычисляем по классической схеме:
Полученные результаты подставим в формулу (1):
б) Вероятность р(Н1/А) находим по формуле Байеса:
|

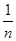 .
. .
. , т.е. вероятность события А равна отношению числа благоприятных случаев для А к общему числу элементарных исходов испытания.
, т.е. вероятность события А равна отношению числа благоприятных случаев для А к общему числу элементарных исходов испытания. .
. .
. , (12)
, (12) ,
,  ,
,  ;
;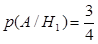 ,
,  ,
,  .
. .
. .
.


