Лекция №13
Тема:Элементы выборочного метода. Генеральная совокупность и выборка. Гистограмма и полигон. Числовые характеристики вариационного ряда: среднее значение, дисперсия, мода, медиана, начальные и центральные моменты, ассиметрия и эксцесс. План:
2 Генеральная совокупность 3 Гистограмма, полигон. 4 Выборочные характеристики выборки. Основные понятия: генеральная совокупность, гистограмма, полигон, выборочные характеристики выборки.
Совокупность всех возможных значений случайной величины х в математической статистике называют генеральной совокупностью. Совокупность n возможных значений х: х1,х2,…,xn, (1) полученных в результате n независимых опытов (наблюдений), называется выборкой или статистическим рядом объема n. Различные значения случайной величины, содержащиеся в выборке (1), называются вариантами. Система вариант a1,a2,…,am, (2) расположенных в возрастающем порядке, называются вариационным рядом. Пусть х – дискретная случайная величина и (2) ее вариационный ряд, полученный по выборке (1). Тогда число
в первой строке которой расположены варианты, а во второй – соответствующие им частоты, называется таблицей частот или эмпирическим законом распределения дискретной случайной величины х. Сумма всех частот в таблице (3) равна единице. Если на плоскости в прямоугольной системе координат построим точки (a i, mi) (i = 1, 2,…, m) и соединим их последовательно отрезками прямых, то получим ломаную линию, которая называется полигоном частот (см.рис. 21)
Полигон частот дает приближенное наглядное представление о характере распре-деления случайной величины х. Если изучаемая случайная величина х непрерывна, то вместо обычного (дискретного) вариационного ряда составляют интервальный вариационный ряд: находят минимальную и максимальную варианты выборки и весь промежуток между ними разбивают на частичные промежутки. Получается так называемый интервальный вариационный ряд: [ c1; c2 [, [ c2; c3 [, …, [ cm; cm+1 ]. (4) Далее по выборке определяют частоту
Интервальная таблица частот графически изображается гистограммой, которая представляет собой ступенчатую линию (см.рис.22). Основанием i -й ступеньки является i -й частичный интервал, а высота hi такова, что площадь ступеньки равна Пример 1. При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка: 10, 13, 10, 9, 9, 12, 12, 6, 7, 9; 8, 9,11, 9, 14, 13, 9, 8, 8, 7; 10, 10, 11, 11, 11, 12, 8, 7, 9, 10; 14, 13, 8, 8, 9, 10, 11, 11, 12, 12. Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон. Решение. а) Выбирая различные варианты из выборки и располагая их в возрастающем порядке, получим вариационный ряд: 6, 7, 8, 9, 10, 11, 12, 13,14. б) Для нахождения частот k i = 1, 3, 6, 8, 6, 6, 5, 3, 2. Таблица частот
в) Полигон изображен на рисунке 23.
Пример 2. Для изучения распределения веса новорожденных были собраны данные для 100 детей и составлена интервальная таблица частот. Для удобства таблица составлена в столбик:
|

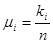 (i = 1,2,…, m), где ki – количество повторений варианты ai в выборке объема n, называется частотой этой варианты в данной выборке.
(i = 1,2,…, m), где ki – количество повторений варианты ai в выборке объема n, называется частотой этой варианты в данной выборке.

 (i = 1,2,…,m) попадания значений х в i- й интервал. Здесь
(i = 1,2,…,m) попадания значений х в i- й интервал. Здесь  - количество членов выборки, попавших в i -й интервал. Если при этом некоторое xk выборки совпадает с граничной точкой между промежутками, то его относят к правому промежутку. В результате получается интервальная таблица частот:
- количество членов выборки, попавших в i -й интервал. Если при этом некоторое xk выборки совпадает с граничной точкой между промежутками, то его относят к правому промежутку. В результате получается интервальная таблица частот:


 . По построению суммарная площадь всех ступенек гистограммы равна 1.
. По построению суммарная площадь всех ступенек гистограммы равна 1. предварительно подсчитаем для каждой варианты соответствующие кратности k i :
предварительно подсчитаем для каждой варианты соответствующие кратности k i :






 Интервалы
веса (кг)
Интервалы
веса (кг)




