Тема: Вероятностное пространство. Элементы комбинаторики
План:
Основные определения: событие, произведение, сумма событий, противоположные события,сочетания и бином Ньютона, перестановки, размещения. Итак, по-прежнему вероятностное пространство есть тройка _ Ω, S, P _, где про Ω уже все сказано — это множество возможных исходов эксперимента, S — совокуп- ность подмножеств Ω, называемых событиями. Событием называется результат некоторого опыта. Событие называется случайным, если в данном опыте оно может наступить, но может и не наступить. Случайные события обозначаем А, В, С,… Событие называется достоверным, если в данном опыте оно обязательно наступит. Достоверное событие обозначаем U. Событие называется невозможным, если в данном опыте оно наступить не может. Невозможное событие обозначаем V . Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем А Ì В. События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В. Суммой событий А и В называется третье событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В. Произведением событий А и В называется третье событие АВ, которое наступает тогда и только тогда, когда оба события: А и В. Понятия суммы и произведения двух событий очевидным образом переносятся на случай любого множества событий. Событием, противоположным событию А, называется событие Условившись обозначать наступление события цифрой «1» и ненаступление – цифрой «0», сумму и произведение двух событий, а также противоположное событие можно определить следующими таблицами:
|
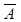, которое наступает тогда и только тогда, когда не наступает событие А.
