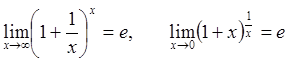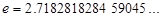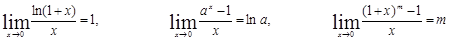Тема: Числовые последовательности и ее предел.
План:
1. Числовые последовательности и ее предел. Единственность предела последовательности.
2. Ограниченность сходящейся последовательности.
3. Свойства сходящихся последовательностей, связанные с неравенствами.
4. Бесконечно малые и бесконечно большие последовательности.
5. Основные свойства бесконечно малых последовательностей.
Ключевые слова: Последовательность, предел, бесконечно большая, бесконечно малая.
Функция, областью определения которой являетсяч множество натуральных чисел, называется последовательностью.
Если по некоторому закону каждому натуральному числу  поставлено в соответствие вполне определенное число
поставлено в соответствие вполне определенное число  то говорят, что задана числовая последовательность
то говорят, что задана числовая последовательность 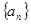 .
.
 :
:
Числа  называются членами последовательности, а число
называются членами последовательности, а число  - общим членом последовательности.
- общим членом последовательности.
Число  называется пределом числовой последовательности
называется пределом числовой последовательности 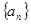 , если если для любого малого числа
, если если для любого малого числа  найдется такой номер
найдется такой номер  (зависящий от
(зависящий от  ), что для всех членов последовательности с номерами
), что для всех членов последовательности с номерами  верно равенство
верно равенство  .Предел
.Предел
числовой последовательности обозначается  .
.
Последовательность имеющая предел называется сходящейся, в противном случае – расходящейся.
Если существуют число  и номер
и номер  такие, что
такие, что 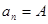 при любом
при любом  , то последовательность
, то последовательность 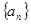 называется финально постоянной.
называется финально постоянной.
Последовательность 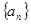 называется ограниченной, если существует число
называется ограниченной, если существует число  такое, что
такое, что  при любом
при любом  .
.
Теорема. 1. Финально постоянная последовательность сходится.
2. Любая окрестность предела последовательности содержит все члены последовательности, за исключением конечного их числа.
3. Последовательность не может иметь двух различных пределов.
4. Сходящаяся последовательность ограничена.
Если 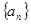 ,
,  - две числовые последовательности, то их суммой, произведением и частным называются соответственно последовательности
- две числовые последовательности, то их суммой, произведением и частным называются соответственно последовательности
 ,
, 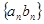 ,
, 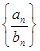
Теорема. Пусть 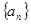 ,
,  - числовые последовательности. Если
- числовые последовательности. Если  ,
, 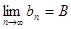 , то
, то
1. 

2. 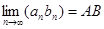
3.  , если
, если 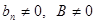
1. Пусть 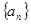 ,
,  - числовые последовательности, причем
- числовые последовательности, причем  ,
, 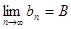 . Если
. Если 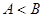 , то начиная с некоторого номера
, то начиная с некоторого номера 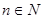 имеет место неравенство
имеет место неравенство 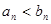
2. Пусть 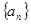 ,
,  и
и 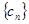 - числовые последовательности и имеет место неравенство
- числовые последовательности и имеет место неравенство  . Тогда, если
. Тогда, если  ,
,  , то.
, то.  .
.
3. Пусть  ,
, 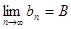 . Если начиная с некоторого номера
. Если начиная с некоторого номера 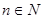
А) 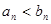 , то
, то 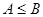
В)  , то
, то 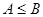
С) 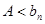 , то
, то 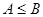
D)  , то
, то 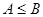
Если каждому элементу 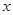 множества
множества  ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент  множества
множества  , то говорят что на множестве
, то говорят что на множестве  задана функция. При этом
задана функция. При этом 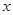 называется независимой переменной или аргументом, а
называется независимой переменной или аргументом, а  - зависимой переменной, а буква
- зависимой переменной, а буква  обозначает закон соответствия.
обозначает закон соответствия.
Множество  называется областью определения или существования функции, а множество
называется областью определения или существования функции, а множество  – областью значений функции.
– областью значений функции.
Существуют следующие способы задания функции
- Аналитический способ, если функция задана формулой вида

- Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента
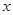 и соответствующие значения функции
и соответствующие значения функции 
- Графический способ состоит в изображении графика функции – множества точек
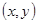 плоскости, абсциссы которых есть значения аргумента
плоскости, абсциссы которых есть значения аргумента 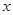 , а ординаты – соответствующие им значения функции
, а ординаты – соответствующие им значения функции 
- Словесный способ, если функция описывается правилом ее составления.
Основные свойства функции
1.Четность и нечетность. Функция называется четной, если для всех значений из области определения  и нечетной, если
и нечетной, если  . В противном случае функция называется функцией общего вида.
. В противном случае функция называется функцией общего вида.
2.Монотонность. Функция  называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке  , если большему значению аргумента из этого пролмежутка соответствует большее (меньшее)значение функции.
, если большему значению аргумента из этого пролмежутка соответствует большее (меньшее)значение функции.
3.Ограниченность. Функция  называется ограниченной на промежутке
называется ограниченной на промежутке  , если существует такое положительное число
, если существует такое положительное число  , что
, что  для любого
для любого 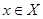 . В противном случае функция называется неограниченной.
. В противном случае функция называется неограниченной.
4.Периодичность. Функция  называется периодической с периодрм
называется периодической с периодрм  , если для любых
, если для любых 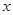 из области определения функции
из области определения функции  .
.
Классификация функций.
1.Обратная функция. Пусть  есть функция от независимой переменной
есть функция от независимой переменной 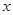 , определенной на множестве
, определенной на множестве  с областью значений
с областью значений  . Поставим в соответствие каждому
. Поставим в соответствие каждому  единственное значение
единственное значение 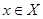 , при котором
, при котором  . Тогда полученная функция
. Тогда полученная функция 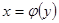 , определенная на множестве
, определенная на множестве  с областью значений
с областью значений  называется обратной.
называется обратной.
2.Сложная функция. Пусть функция  есть функция от переменной
есть функция от переменной 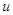 ,
,
определенной на множестве  с областью значений
с областью значений  , а переменная
, а переменная 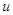 в свою
в свою
очередь является функцией.
Число  называется пределом функции
называется пределом функции  при
при  , если для любого малого числа
, если для любого малого числа  найдется такое положительное число
найдется такое положительное число  , что для всех
, что для всех 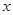 таких,что
таких,что  верно неравенство
верно неравенство  .
.
Предел функции в точке. Пусть функция  задана в некоторой окрестности точки
задана в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  . Число
. Число  называется пределом функции
называется пределом функции  при
при 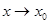 , если для любого, даже сколь угодно малого
, если для любого, даже сколь угодно малого  , найдется такое положительное число
, найдется такое положительное число  (зависящий от
(зависящий от  ), что для всех
), что для всех 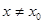 и удовлетворяющих условию
и удовлетворяющих условию  выполняется неравенство
выполняется неравенство  . Этот предел обозначается
. Этот предел обозначается  .
.
Функция  называется бесконечно малой величиной при
называется бесконечно малой величиной при 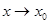 , если ее предел равен нулю.
, если ее предел равен нулю.
Свойства бесконечно малых величин
1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Первый замечательный предел


и второй замечательный предел
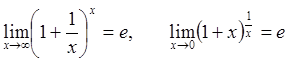
где 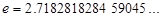
помогают при вычислении многих пределов.
Также при вычислении пределов бывает полезным знание следующих пределов 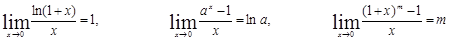

 поставлено в соответствие вполне определенное число
поставлено в соответствие вполне определенное число  то говорят, что задана числовая последовательность
то говорят, что задана числовая последовательность 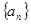 .
. :
: называются членами последовательности, а число
называются членами последовательности, а число  называется пределом числовой последовательности
называется пределом числовой последовательности  найдется такой номер
найдется такой номер  (зависящий от
(зависящий от  ), что для всех членов последовательности с номерами
), что для всех членов последовательности с номерами  верно равенство
верно равенство  .Предел
.Предел .
.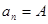 при любом
при любом  такое, что
такое, что  при любом
при любом  .
. - две числовые последовательности, то их суммой, произведением и частным называются соответственно последовательности
- две числовые последовательности, то их суммой, произведением и частным называются соответственно последовательности ,
, 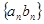 ,
, 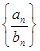
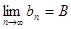 , то
, то

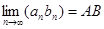
 , если
, если 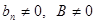
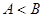 , то начиная с некоторого номера
, то начиная с некоторого номера 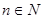 имеет место неравенство
имеет место неравенство 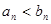
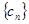 - числовые последовательности и имеет место неравенство
- числовые последовательности и имеет место неравенство  . Тогда, если
. Тогда, если  , то.
, то.  .
.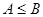
 , то
, то 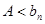 , то
, то  , то
, то 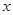 множества
множества  ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент  множества
множества  , то говорят что на множестве
, то говорят что на множестве  обозначает закон соответствия.
обозначает закон соответствия.

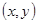 плоскости, абсциссы которых есть значения аргумента
плоскости, абсциссы которых есть значения аргумента  и нечетной, если
и нечетной, если  . В противном случае функция называется функцией общего вида.
. В противном случае функция называется функцией общего вида. для любого
для любого 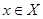 . В противном случае функция называется неограниченной.
. В противном случае функция называется неограниченной. , если для любых
, если для любых  .
. единственное значение
единственное значение  . Тогда полученная функция
. Тогда полученная функция 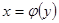 , определенная на множестве
, определенная на множестве 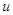 ,
, с областью значений
с областью значений  , если для любого малого числа
, если для любого малого числа  верно неравенство
верно неравенство  .
. , кроме, быть может, самой точки
, кроме, быть может, самой точки 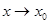 , если для любого, даже сколь угодно малого
, если для любого, даже сколь угодно малого  (зависящий от
(зависящий от 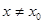 и удовлетворяющих условию
и удовлетворяющих условию  выполняется неравенство
выполняется неравенство  .
. называется бесконечно малой величиной при
называется бесконечно малой величиной при