Статистики
Мы можем вычислить средние, медианы, дисперсии и процентили по данным, собранным из совокупности. Значения различных описательных мер, вычисленных для генеральных совокупностей, называются параметрами. Для выборок те же описательные меры называются статистиками. Параметр описывает совокупность так же, как статистика – выборку. Принято обозначать статистики латинскими буквами, а параметры – греческими. Символ X принят для выборочного среднего, а греческая буква М обозначает генеральное среднее. Выборочная дисперсия обозна-чается D или Статистику, вычисленную по выборке, можно рассматривать как оценку параметра совокупности. Оцениватель – некоторая функция от значений в выборке, дающая величину, называемую оценкой; оценка же дает некоторую информацию о параметре. Например, выборочное среднее X – оцениватель среднего или среднего значения совокупности. Меры центральной тенденции К мерам центральной тенденции (или мерам положения) относятся: мода, медиана и средние величины. Мер положения много, но каждая из них преимущественно используется только в определенных условиях.
Мода
Мода – такое значение в множестве наблюдений, которое встречается наиболее часто. Пример: 2, 6, 6, 9, 9, 9, 10. Мо = 9. Мода (Мо) – это мера положения, определяемая как значение варианты, наиболее часто встречающееся в выборке. Варианта – это переменная, представляющая собой результаты измерений, которые варьируются, т.е. изменяются. Мода, уже известная нам по системам классифицированных и упорядоченных событий, – это значение случайной величины, имеющее наибольшую вероятность появления. Мода служит единственно возможной мерой положения для существенно дискретной случайной величины. Соглашение об использовании моды: 1. В том случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа оценок не имеет моды. Пример: 0,5; 0,5; 1,6; 1,6; 2,9; 2,9. Моды нет. Мо = 0. 2. Когда два соседних значения имеют одинаковую частоту, и они больше частоты любого другого значения, мода есть среднее этих двух значений. Пример: 1, 1, 2, 2, 2, 3, 3, 3, 4. Мо = 2,5. 3. Если два несмежных значения в группе имеют равные частоты и они больше частоты любого другого значения, то имеем две моды. Говорят: группа оценок является бимодальной. Пример: 10, 11, 11, 11, 12, 13, 14, 14, 14, 15. Мо = 11 и 14. Для непрерывных случайных величин, имеющих “выпуклую” функцию распределения, мода определяется из условия максимума функции. Для квантованных непрерывных случайных величин с “выпуклой” гистограммой за моду приближенно принимается среднее значение классового интервала. Необходимо отметить, что среди распределений встречаются унимодальные, у которых мода отсутствует (рис. 6, а), и полимодальные, у которых две и более мод (рис. 6, б).
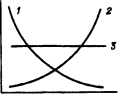
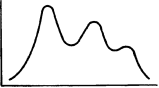
а б Рис. 6. Унимодальные распределения (а, кривые 1, 2, 3
|

 , а генеральная σ2.
, а генеральная σ2.