I. Задача о массе материальной пластины
Определение 1. Разбиением T простого компакта DÌR2 будем называть любое представление его в виде объединения конечного числа квадрируемых компактов (D SK) попарно без общих внутренних точек. Эти компакты (D SK) назовем ячейками разбиения T компакта D, а площадь ячейки (D SK) обозначим через D SK ( Определение 2. Диаметром l(T ) разбиения T простогокомпакта D будем называть наибольший из диаметров его ячеек:
0 x Очевидно, что для любого простого компакта DÌ; R 2 можно указать разбиение T со сколь угодно малым диаметром. Наиболее удобным является разбиение с помощью прямых, параллельных осям координат.
Определение 3. Пусть в плоскости OXY расположена материальная пластина D (представляющая собой простой компакт) c поверхностной плотностью m(x0;y0) распределения масс в точке P0(x0;y0) пластины D называется предел
где D - любая квадрируемая часть пластины D, содержащая точку P0, а SD, m(D), l(D) - соответственно площадь, масса и диаметр этой части D пластины D.
Если пластина D однородная, т.е. Пусть теперь пластина D неоднородная, т.е. Возьмем произвольное (достаточно мелкое) разбиение T пластины D на любое конечное число n ячеек (D Sk) (попарно без общих внутренних точек) с площадями D Sk (
Определение 4. Массой m материальной пластины D называется предел суммы (1) при
Пределы вида (2) носят название двойных интегралов.
|


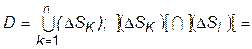 Ø, i¹k;
Ø, i¹k; 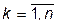 .
. ).
).






 y
y



 ,
, , то ее масса m равна
, то ее масса m равна  .
. в D.
в D. , тогда масса всей пластины D будет приближенно равна
, тогда масса всей пластины D будет приближенно равна
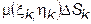 . (1)
. (1)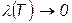 (если этот предел существует и конечен):
(если этот предел существует и конечен): . (2)
. (2)


