B Аналогично вводится понятие компакта, правильного в напра
0 Рис.1 x Примерами правильных компактов в направлении обеих осей являются, например, эллипс, круг, треугольник. Теорема 1. Пусть функция f(x; y) интегрируема в прямоугольнике
и при любом фиксированном x
Тогда
т.е. . Заметим, что правую часть равенства (2) обычно записывают в виде
что
Правую часть последнего равенства называют повторным интегралом. à Пусть выполнены условия теоремы. Согласно определению двойного интеграла имеем
где s - интегральная сумма для функции f(x; y), соответствующая произвольному разбиению прямоугольника П на любое конечное число квадрируемых ячеек при любом выборе точек Учитывая это, возьмем в качестве Т разбиение прямоугольника П на прямоугольные ячейки качестве точек
Рис. 2 Площадь ячейки Это разбиение T порождает соответственно разбиения T1 и T2 соответственно отрезков
Пусть Очевидно,
Так как
то
Поскольку, далее
то из соотношения
Последнее неравенство этой цепочки запишем подробнее в виде:
Зафиксируем теперь разбиение Т1 отрезка Так как
Последнее неравенство справедливо для любого фиксированного разбиения Т1 отрезка Таким образом,
а это и значит, что
или
Замечание 1. Аналогично можно показать, что
при условии, что существуют двойной интеграл Из формул (3) и (6) при выполнение соответствующих условий получаем формулу изменения порядка интегрирования в повторном интеграле (в случае прямоугольной области):
Последнее соотношение заведомо имеет место, если функция f(x; y) непрерывна в прямоугольнике П. Теорема 2 (общий случай). Пусть D – правильный в направлении оси Oy простой компакт, ограниченный линиями x=a, x=b, y=j1(x), y=j2(x), где j1(x) и j2(x) – непрерывные на отрезке [a;b]
Тогда
y
0 a b x y=j1(x) Рис.3 à Пусть выполнены условия теоремы. Возьмем любой прямоугольник П, содержащий компакт D и имеющий ту же проекцию на ось Ox, что и компакт D, т.е. отрезок [a;b]. Пусть отрезок Введем в рассмотрение функцию
Проверим, что функция F(x;y) в прямоугольнике П удовлетворяет всем условиям теоремы1. Функция F(x;y) интегрируема на каждом из компактов D и [П \D ], так как на компакте D
Следовательно, по свойству аддитивности, функция F(x;y) интегрируема в П, причем т.е.
Кроме того, при любом фиксированном
т.е.
Применяя к функции F(x;y) на П теорему 1 и учитывая (11), получим:
Из (10) и (12) следует (9).¨
осей, изображена на Рис.4.
0 1 x Рис.4 Имеем
0 x Рис.5 Пусть, далее, функция f(x;y) интегрируема в D и при любом фиксированном
Если компакт правильный в направлении обеих осей, то (при выполнении соответствующих условий) имеют место обе формулы (9) и (13) и, следовательно,
Формула (14) называется формулой изменения порядка интегрирования в повторном интеграле. Замечание 3. Если компакт D неправильный, то его стараются разбить (если это возможно) на конечное число компактов D1,D2,…,Dn, правильных в направлении той или иной оси, затем записывают равенство
после чего каждый из интегралов в правой части (15) вычисляют по одной из формул (9) или (13). Замечание 4. Для упрощения вычислений бывает удобнее иногда и правильный компакт D разбить на боле мелкие компакты. Так поступают, например, когда требуется изменить порядок интегрирования в повторном интеграле, когда участок границы компакта D, состоящий из точек входа (выхода) задается различными уравнениями на различных его частях. Например, пусть компакт D ограничен линиями
y
Рис.6
Тогда С другой стороны, , Таким образом,
|

 D D влении оси OX.
D D влении оси OX. A2 P1
A2 P1
 существует интеграл
существует интеграл . (1)
. (1) ,
, . (2)
. (2) , так,
, так, . (3)
. (3)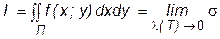
 ,
, этих ячеек, а
этих ячеек, а 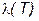 - диаметр разбиения Т.
- диаметр разбиения Т.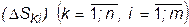 с помощью прямых, параллельных осям координат (см.Рис. 2), а в
с помощью прямых, параллельных осям координат (см.Рис. 2), а в




 Y
Y 



 ym=d
ym=d ym-1
ym-1  yi
yi  y2
y2

 y1
y1 c
c 0 a x1 xk-1 xk xn-1 b=xn x
0 a x1 xk-1 xk xn-1 b=xn x равна
равна  .
. и
и  :
: ,
, .
. – наибольшая из длин частичных отрезков разбиения Т1 отрезка
– наибольшая из длин частичных отрезков разбиения Т1 отрезка  - наибольшая из длин частичных отрезков разбиения Т2 отрезка
- наибольшая из длин частичных отрезков разбиения Т2 отрезка 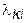 - диаметр ячейки
- диаметр ячейки  .
. ,
, . (4)
. (4) ,
, ,с учетом (4), следует, что
,с учетом (4), следует, что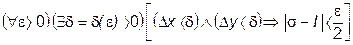 .
. . (5)
. (5) , а разбиение T2 отрезка
, а разбиение T2 отрезка  .
. при
при 
 .
.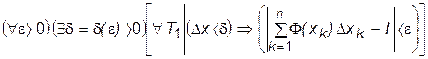 ,
, , т.е.
, т.е. 
 . ¨
. ¨ (6)
(6) и при любом фиксированном
и при любом фиксированном  определенный интеграл
определенный интеграл  .
. . (7)
. (7) функции, причем j1(x) £ j2(x) на [a;b]. Пусть, далее, функция fx;y) интегрируема в D и при любом фиксированном
функции, причем j1(x) £ j2(x) на [a;b]. Пусть, далее, функция fx;y) интегрируема в D и при любом фиксированном 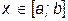 существует определенный интеграл
существует определенный интеграл . (8)
. (8)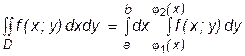 . (9)
. (9) y=j2(x)
y=j2(x)



 d
d D
D

 с
с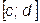 - проекция прямоугольника П на ось Oy. (см. Рис.3)
- проекция прямоугольника П на ось Oy. (см. Рис.3)
 - интегрируемая функция по условию, а на компакте [П \D ] - функция F(x;y) непрерывна, исключая быть может, точки линий y=j1(x) и y=j2(x), имеющих нулевую площадь. Поэтому
- интегрируемая функция по условию, а на компакте [П \D ] - функция F(x;y) непрерывна, исключая быть может, точки линий y=j1(x) и y=j2(x), имеющих нулевую площадь. Поэтому .
. ,
, . (10)
. (10) функция F(x,y) интегрируема на
функция F(x,y) интегрируема на  , причем
, причем  =
= ,
, . (11)
. (11) . (12)
. (12)


 Пример. Вычислим интеграл
Пример. Вычислим интеграл  , где область интегрирования D ограничена линиями
, где область интегрирования D ограничена линиями 
 y
y 
 àОбласть интегрирования D, правильная в направлении обеих
àОбласть интегрирования D, правильная в направлении обеих
 Воспользуемся для вычисления формулой (9), где
Воспользуемся для вычисления формулой (9), где .
.
 Замечание 2. Пусть D – правильный в направлении оси OX простой компакт (см.Рис.5), ограниченный линиями
Замечание 2. Пусть D – правильный в направлении оси OX простой компакт (см.Рис.5), ограниченный линиями  , где y1 (y) и y2(y) непрерывные на отрезке
, где y1 (y) и y2(y) непрерывные на отрезке  функции, y1 (y) £ y2(y)
функции, y1 (y) £ y2(y)  .
. y
y 






 d
d 

 D
D

 c
c существует определенный интеграл
существует определенный интеграл  . Тогда
. Тогда . (13)
. (13) . (14)
. (14) , (15)
, (15) (см.Рис.6) и функция f(x;y) интегрируема в D.
(см.Рис.6) и функция f(x;y) интегрируема в D.


 y =-x y=x
y =-x y=x






 1
1
 D1 D2
D1 D2 -1 0 1 x
-1 0 1 x .
.
 =
=  .
.


