Основные свойства двойного интеграла
Пусть D – простой компакт в R2 . Имеют место следующие утверждения. 1. Если функция f (x; y) интегрируема в D и c = const ÎR, то функция c×f (x; y) также интегрируема в D и
2. Если функции f (x; y) и j(x; y) интегрируемы в D, то их сумма также интегрируема в D и Замечание. Это свойство методом математической индукции обобщается на случай любого конечного числа интегрируемых функций. 3. Свойство аддитивности: Если компакт D есть объединение простых компактов D1 и D2. (
4. Если функция f (x;y) интегрируема в D и f (x; y) ³0 в D (f (x; y)£0 в D), то
5. Если функции f (x; y) и j(x; y) интегрируемы в D и f (x; y)£ j(x; y) в D, то
6. Если функция f (x; y) интегрируема в D и m £ f (x; y) £ M в D, то
Доказательство утверждений 1-6 аналогично доказательству соответствующих утверждений функций одной переменной. 7. Теорема о среднем значении для непрерывной функции: Если функция f (x; y) непрерывна на связном простом компакте D, то существует по крайней мере одна точка (x0;y0)ÎD, такая, что
При этом число àТак как функция f (x; y) непрерывна на компакте D
Отсюда
Следовательно,
Число
Отсюда и следует (1). 8. Теорема об оценке двойного интеграла: Если функция f (x; y) интегрируема в D, то функция
à Так как
Последнее двойное неравенство равносильно (2).¨
|

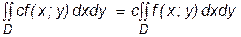 .
. .
. ) без общих внутренних точек и функция f (x; y) интегрируема в D, то она интегрируема на каждом из компактов D1 и D2, причем
) без общих внутренних точек и функция f (x; y) интегрируема в D, то она интегрируема на каждом из компактов D1 и D2, причем .
. (
( ).
). .
.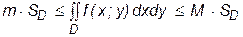 .
. .
.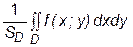 называется средним значением функции f на компакте D.
называется средним значением функции f на компакте D. , то она принимает на нем свои наименьшее и наибольшее значения: m и M соответственно. Поэтому
, то она принимает на нем свои наименьшее и наибольшее значения: m и M соответственно. Поэтому .
.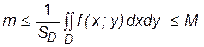 .
. ,
,  .
. также интегрируема в D, причем
также интегрируема в D, причем .
.
 , то
, то .
.


