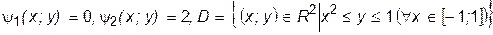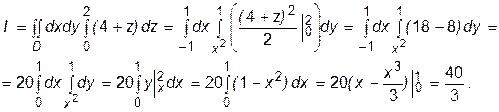Понятие тройного интеграла
Пусть даны кубируемое тело Q и функция f (x;y;z), определенная в Q. Будем предполагать, что Q – связный простой компакт. Разобьем тело Q на любое конечное число n кубируемых частей (ячеек) (DVk) попарно без общих внутренних точек:
Это разбиение будем обозначать через T. Введем следующие обозначения: DVk – объем ячейки (DVk) ( В каждой ячейке (DVk) возьмем произвольно точку Pk(xk; hk: gk). Вычислим значение функции f в точках Pk и составим интегральную сумму:
Определение. Если при
Справедливы следующие условия интегрируемости функций трех переменных: Теорема 1(необходимое условие интегрируемости). Если функция f(x; y;z) интегрируема на простом компакте D, то она ограничена на этом компакте. Теорема 2(необходимое и достаточное условие интегрируемости). Для того, чтобы ограниченная на простом компакте D функция f(x; y;z) была интегрируема на этом компакте, необходимо и достаточно, чтобы Теорема 3 (достаточное условие интегрируемости). Если функция f (x; y;z) непрерывна на компакте D, то она интегрируема на этом компакте. Доказательство этих утверждений аналогично доказательству соответствующих теорем для функций двух переменных. Тройные интегралы обладают следующими свойствами: Пусть Q – простой компакт в R3. Имеют место следующие утверждения: 1. Если функция f (x; y; z) интегрируема в Q и c = const ÎR, то функция c×f (x; y;z) также интегрируема в Q и
2. Если функции f (x; y;z) и j(x; y;z) интегрируемы в Q, то их сумма также интегрируема в Q и Замечание. Это свойство методом математической индукции обобщается на случай любого конечного числа интегрируемых функций. 3. Свойство аддитивности: Если компакт Q есть объединение простых компактов Q1 и Q2. (
4. Если функция f (x;y;z) интегрируема в Q и f (x; y;z) ³0 в Q (f (x; y;z)£0 в Q ), то
5. Если функции f (x; y;z) и j(x; y;z) интегрируемы вQи f (x; y;z)£ j(x; y;z) в D, то
6. Если функция f (x; y;z) интегрируема в Q и m £ f (x; y;z) £ M в D, то
Доказательство утверждений 1-6 аналогично доказательству соответствующих утверждений для функций одной переменной. 7. Теорема о среднем значении для непрерывной функции: Если функция f (x; y;z) непрерывна на связном простом компакте Q, то существует по крайней мере одна точка (x0;y0;z0)ÎQ, такая, что
При этом число 8. Теорема об оценке тройного интеграла: Если функция f (x; y;z) интегрируема в Q, то функция
[n1] §2. Вычисление тройных интегралов
I. В простейших случаях (при удачном разбиении тела Q на ячейки и выборе точек Pk в этих ячейках) тройной интеграл
можно вычислить, используя определение тройного интеграла. На практике, как правило, вычисление тройного интеграла (1) сводится к вычислению одного определенного интеграла и одного двойного интеграла. В итоге тройной интеграл вычисляется с помощью 3-х последовательных однократных (определенных) интегралов. Справедлива следующая Теорема. Пусть тело Q - правильный в направлении оси Oz простой компакт и D – его проекция на плоскость OXY. Пусть это тело ограничено поверхностями
Замечание. Иногда внутреннее интегрирование удобнее вести по x или по y (в зависимости от строения тела Q). Пример. Вычислим тройной интеграл
где тело Q ограничено поверхностями
y
x y=x2 Рис.1 В данном случае Имеем ¨
|

 Ø
Ø  .
. ), l(T) – наибольший из диаметров ячеек разбиения T.
), l(T) – наибольший из диаметров ячеек разбиения T. . (1)
. (1) существует конечный предел интегральной суммы (1) (не зависящий ни от способа разбиения тела Q на ячейки, ни от выбора точек Pk в этих ячейках), то функция f (x,y,z), называется интегрируемой в Q, а сам этот предел называется тройным интегралом от функции f по компакту Q:
существует конечный предел интегральной суммы (1) (не зависящий ни от способа разбиения тела Q на ячейки, ни от выбора точек Pk в этих ячейках), то функция f (x,y,z), называется интегрируемой в Q, а сам этот предел называется тройным интегралом от функции f по компакту Q: , (2)
, (2) , где
, где  и
и  соответственно верхняя и нижняя суммы Дарбу функции f (x; y;z), соответствующие разбиению T компакта D.
соответственно верхняя и нижняя суммы Дарбу функции f (x; y;z), соответствующие разбиению T компакта D. .
.
 .
.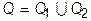 ) без общих внутренних точек и функция f (x; y;z) интегрируема на Q, то она интегрируема на каждом из компактов Q1 и Q 2, причем
) без общих внутренних точек и функция f (x; y;z) интегрируема на Q, то она интегрируема на каждом из компактов Q1 и Q 2, причем
 .
. .
. .
. .
. .
. называется средним значением функции f на компакте Q.
называется средним значением функции f на компакте Q. также интегрируема в Q, причем
также интегрируема в Q, причем .
.
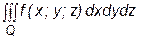
 (
( )и цилиндрической поверхностью с направляющей ¶D и образующей, параллельной оси Oz. Пусть, далее, функции y1(x, y) и y2(x, y) непрерывны в D и функция
)и цилиндрической поверхностью с направляющей ¶D и образующей, параллельной оси Oz. Пусть, далее, функции y1(x, y) и y2(x, y) непрерывны в D и функция  непрерывна в Q. Тогда
непрерывна в Q. Тогда . (2)
. (2) ,
, .
.


 z à Воспользуемся формулой (2), учитывая, что Q -
z à Воспользуемся формулой (2), учитывая, что Q - z=2 правильный в направлении оси Оz простой компакт
z=2 правильный в направлении оси Оz простой компакт
 y=x2 y=1 (см.Рис.1).
y=x2 y=1 (см.Рис.1).