Вычисление площадей плоских фигур и объемов тел
I. Площадь плоской квадрируемой фигуры D (простого компакта в R2)
Рис.1
Пример 1. Вычислим площадь фигуры D, ограниченной линиями
0 1 2 4 x x+y=4 Рис.2 Имеем:
¨ Пример 2. Вычислим площадь фигуры D, ограниченной линиями
0 4 x Используя формулу (1) и переходя к полярным координатам
r =2cosj Рис.3
¨ II. Объем Q (простого компакта в R3) равен тройному интегралу
Рис.4 Пусть Q - правильный в направлении оси OZ компакт и D - его проекция на плоскость OXY). Если этот компакт ограничен поверхностями
Отсюда непосредственно вытекает следующее утверждение, выражающее геометрический смысл двойного интеграла: Если функция f (x; y) непрерывна и неотрицательна на простом компакте D, то криволинейное цилиндрическое тело (см.Рис.5), ограниченное плоскостью OXY, сверху – графиком функции z= f (x; y), а с боков – цилиндрической поверхностью с направляющей
z
D
x Рис. 5 Пример 3. Вычислим объем тела Q, ограниченного плоскостями
à Тело Q - правильный в направлении оси компакт, его проекция на плоскость есть квадрат:
x A(4;4) Рис.6
Имеем:
¨ Замечание. В ряде случаев объем тела Q можно вычислить с помощью определенного интеграла. Например, Упражнения I. Вычислите площади плоских областей, ограниченных линиями: 1) 2) 3) 4) 5) II. Вычислите объемы тел, ограниченных указанными поверхностями: 1) параболоидами 2) цилиндрами 3) сферой 4) параболоидом
|

 R2 можно вычислить по формуле (см. главу 1, §1)
R2 можно вычислить по формуле (см. главу 1, §1) . (1)
. (1)


 y Отсюда, в частности, для правильного в направлении оси OY
y Отсюда, в частности, для правильного в направлении оси OY


 D компакта D получаем известную формулу
D компакта D получаем известную формулу
 (см. Рис. 1).
(см. Рис. 1). a b x
a b x
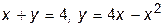 .
.



 оси OY компактом. Его проекция на ось OX
оси OY компактом. Его проекция на ось OX D есть отрезок [1;4].
D есть отрезок [1;4].

 .
.
 j =const компакт, ограниченный линиями r =2cosj (линия
j =const компакт, ограниченный линиями r =2cosj (линия

 входа), r = 4cosj (линия выхода) и лучами
входа), r = 4cosj (линия выхода) и лучами
 j = -p/2;j = p/2;
j = -p/2;j = p/2; будем иметь:
будем иметь:
 (см.гл. 2, § 1):
(см.гл. 2, § 1):
 . (2)
. (2)





 y
y


 D
D x
x непрерывны в D и
непрерывны в D и  и цилиндрической поверхностью с направляющей
и цилиндрической поверхностью с направляющей  и образующей, параллельной оси OZ (см. Рис. 4), то
и образующей, параллельной оси OZ (см. Рис. 4), то
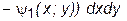 .
. и образующей, параллельной оси OZ, имеет объем
и образующей, параллельной оси OZ, имеет объем . (3)
. (3) z= f (x; y),
z= f (x; y), 



 y
y и параболоидом
и параболоидом  .
. .
.



 D
D





 4
4
 , где
, где  – проекция тела Q на ось Ox, а
– проекция тела Q на ось Ox, а  - площадь фигуры, полученной при пересечении тела Q плоскостью, перпендикулярной оси Ox и проходящей через точку этой оси с абсциссой
- площадь фигуры, полученной при пересечении тела Q плоскостью, перпендикулярной оси Ox и проходящей через точку этой оси с абсциссой 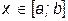 .
. ;
; ;
;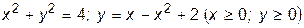 ;
; ;
;
 и плоскостями
и плоскостями 
 и плоскостями
и плоскостями 
 и параболоидом
и параболоидом  (внутренний по отношению к параболоиду;
(внутренний по отношению к параболоиду; и сферой
и сферой  .
.


