Вычисление площади ограниченного участка поверхности
I. Определение площади участка поверхности s как предела площади вписанной многогранной поверхности при стремлении к нулю наибольшего из диаметров граней неприменимо. Это определение теряет смысл даже для очень простых поверхностей. Как показал в 1880г. немецкий математик Шварц даже для такой простой поверхности как боковая поверхность прямого кругового цилиндра указанного выше предела не существует. В данном параграфе приводится общепринятый ныне способ введения понятия площади гладкой поверхности и ее вычисления. Пусть в пространстве относительно заданной прямоугольной системы координат OXYZ дана ограниченная связная поверхность (s), являющаяся графиком функции
Пусть, далее, D – проекция этой поверхности на плоскость OXY, а функция f (x;y) непрерывно-дифференцируема в D. Следовательно, в каждой точке поверхности (s) существует касательная плоскость к ней, не параллельная оси OZ. Кроме того, будем предполагать, что D – простой компакт в R2. Разобьем произвольным образом D на любое конечное число n квадрируемых ячеек Проведем через каждую точку Mk касательную плоскость к (s) и выделим на ней ячейку Ячейки Площадь этой поверхности равна
Пусть l(T ) – наибольший из диаметров ячеек( Определение. Если при Таким образом, по определению,
Справедлива следующая Теорема. Если поверхность (s) является графиком непрерывно-дифференцируемой в D функцией (1), то поверхность s квадрируема, причем
à Из курса геометрии известно, что:
где gk - величина острого угла между плоскостью OXY и касательной плоскостью к поверхности (s) в точке Mk. Из (5) имеем:
Для вычисления
и
где Найдем скалярное произведение этих векторов. Имеем
С другой стороны,
Следовательно,
откуда
Поэтому, с учетом (6), имеем
Отсюда видим, что s* есть интегральная сумма для непрерывной в D функции Следовательно, существует конечный предел
Другими словами, поверхность (s) квадрируема и ее площадь
Пример 1. Вычислим площадь части сферы
à z
x Рис. 7 à Так как указанная в условии задачи часть сферы симметрична относительно плоскости OXY, то
Имеем
Учитывая, что
получим
Следовательно,
II. Выведем теперь формулу для вычисления площади поверхности (s), образованной вращением кусочно-гладкой дуги Уравнение этой поверхности в R3 относительно прямоугольной системы координат OXYZ имеет вид:
D z Рис. 8 Поскольку то
а тогда вся искомая площадь
Замечание. Если дуга Пример. Найдем площадь сферического пояса, полученного вращением полуокружности
à Воспользуемся формулой (7). Имеем
-R 0 a b R x Рис.9
Следовательно,
В частности, если Упражнения 1. Вычислите площадь поверхности конуса 2. Найти площадь поверхности, вырезанную цилиндром 3. Найти площадь части поверхности
|

 . (1)
. (1) попарно без общих внутренних точек и с площадями
попарно без общих внутренних точек и с площадями  . Это разбиение обозначим через T. В каждой ячейке
. Это разбиение обозначим через T. В каждой ячейке  и на поверхности s соответственно точки
и на поверхности s соответственно точки  .
. , проекция которой на плоскость OXY есть
, проекция которой на плоскость OXY есть  .Площадь ячейки
.Площадь ячейки  .
. . (2)
. (2) ).
). существует конечный предел s площади чешуйчатой поверхности (s*), то этот предел называется площадью поверхности (s), а сама эта поверхность называется квадрируемой.
существует конечный предел s площади чешуйчатой поверхности (s*), то этот предел называется площадью поверхности (s), а сама эта поверхность называется квадрируемой. . (3)
. (3) . (4)
. (4) , (5)
, (5) . (6)
. (6) заметим, что угол gk равен углу между векторами
заметим, что угол gk равен углу между векторами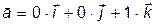
 ,
, -вектор, перпендикулярный плоскости OXY,
-вектор, перпендикулярный плоскости OXY,  - вектор, перпендикулярный касательной плоскости к (s) в точке Mk.
- вектор, перпендикулярный касательной плоскости к (s) в точке Mk. .
. .
. =1,
=1, .
. .
. .
. .
. .
. , заключенной внутри цилиндра
, заключенной внутри цилиндра  (см. Рис. 7).
(см. Рис. 7).


 y
y

















 , где s1 – площадь части полусферы
, где s1 – площадь части полусферы  , заключенной внутри цилиндра
, заключенной внутри цилиндра  Проекция этой части полусферы на плоскость OXY есть круг
Проекция этой части полусферы на плоскость OXY есть круг R2
R2 
 .
.
 .
. ,
,

 ¨
¨ вокруг оси OX (см. Рис. 8).
вокруг оси OX (см. Рис. 8). . Возьмем часть этой поверхности, расположенную в полупространстве
. Возьмем часть этой поверхности, расположенную в полупространстве  . Ее уравнение
. Ее уравнение  , а площадь
, а площадь  .
.






 y
y







 ,
,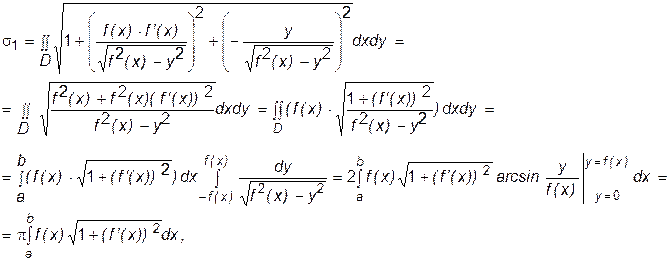
 . (7)
. (7) пересекает отрезок
пересекает отрезок  в конечном числе точек, то площадь поверхности, образованной вращением этой дуги вокруг оси OX может быть вычислена по формуле
в конечном числе точек, то площадь поверхности, образованной вращением этой дуги вокруг оси OX может быть вычислена по формуле  .
. вокруг оси Ox.
вокруг оси Ox. ,
, 


 ,
,
 .
. .
. ,то
,то  - площадь поверхности шара радиуса R.¨;
- площадь поверхности шара радиуса R.¨; , заключенной внутри цилиндра
, заключенной внутри цилиндра 
 из сферы
из сферы  .
. , вырезанной цилиндром
, вырезанной цилиндром 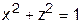 и расположенной в первой октанте.
и расположенной в первой октанте.


