II. Замена переменных в тройном интеграле
Определение. Отображение F
тела 1) Это отображение взаимно-однозначно; 2) отображение F непрерывно-дифференцируемо в Q*,т.е. (функции 3) якобиан отображения F отличен от нуля и в Q*:
Справедливо следующее утверждение: Теорема. Если отображение F компакта Q* на Q регулярно, то
Замечание. Формула (2) имеет место и в случае, когда якобиан отображения (1) в отдельных точках, линиях или на поверхностях с нулевым объемом обращается в нуль, а само отображение не является взаимно-однозначным на границе тела Q. Часто вычисление тройного интеграла значительно упрощается, если перейти от декартовых координат к цилиндрическим или сферическим. 1. Тройной интеграл в цилиндрических координатах Пусть x,y,z – декартовы координаты точки
z
x Рис.2 Декартовы координаты точки M связаны с цилиндрическими координатами этой точки равенствами:
Якобиан отображения (3) равен r.
Формула замены переменных в тройном интеграле при переходе от декартовых координат к цилиндрическим принимает вид:
Пример. Вычислим тройной интеграл
х Рис.3
Тело Q –правильный в направлении оси Oz простой компакт. Его проекция на плоскость OXY есть круг:
Переходя к цилиндрическим координатам и используя формулу (4). будем иметь:
¨;
|

 (1)
(1) на тело
на тело  называется регулярным, если:
называется регулярным, если: имеют в Q* непрерывные частные производные 1-го порядка
имеют в Q* непрерывные частные производные 1-го порядка .
. (2)
(2) R3 относительно заданной прямоугольной сиcтемы координат OXYZ. Цилиндрические координаты этой точки - это тройка чисел r, j, z, где r, j - полярные координаты точки P (проекции точки M на плоскость OXY), а z - обычная декартова апликата z точки M ( см.Рис. 2).
R3 относительно заданной прямоугольной сиcтемы координат OXYZ. Цилиндрические координаты этой точки - это тройка чисел r, j, z, где r, j - полярные координаты точки P (проекции точки M на плоскость OXY), а z - обычная декартова апликата z точки M ( см.Рис. 2). z
z
 M
M


 y y
y y j r
j r
 x P
x P . (3)
. (3) .
. . (4)
. (4) , где
, где (см. Рис. 3).
(см. Рис. 3).
 z=2
z=2


 D
D 2z = x2+y2
2z = x2+y2

 0 y 2 x
0 y 2 x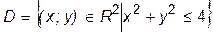 .
.




