Пусть (x;y;z) декартовы координаты точки  R3. Сферические координаты точки М - числа r, q, j, где r – расстояние от точки M до начала координат (длина радиуса-вектора
R3. Сферические координаты точки М - числа r, q, j, где r – расстояние от точки M до начала координат (длина радиуса-вектора  ), q - величина угла (в радианах), образованного лучом OM с положительным направлением оси OZ, а j - величина угла, образованного лучом OP (P – проекция точки M на плоскость OXY) с положительным направлением оси OX ( см. Рис.4).
), q - величина угла (в радианах), образованного лучом OM с положительным направлением оси OZ, а j - величина угла, образованного лучом OP (P – проекция точки M на плоскость OXY) с положительным направлением оси OX ( см. Рис.4).
Очевидно, легко видеть, что  для
для 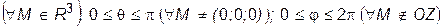
 z
z


 M
M
 q r Z
q r Z




 0 y y
0 y y
 j
j

 x P
x P
x Рис. 4
Декартовы координаты x;y;z точки M связаны со сферическими координатами r, q, j этой точки соотношениями
 . (5)
. (5)
Вычислим Якобиан отображения (5).
Имеем:

и, следовательно,  .
.
Формулу (3) замены переменных в тройном интеграле при переходе от декартовых
координат к сферическим теперь можно записать в виде:
 . (6)
. (6)
Замечание. Формулой (6) удобно пользоваться тогда, когда  или когда область интегрирования есть шар
или когда область интегрирования есть шар  .
.
Легко видеть, что множество всех точек  R3 таких, что
R3 таких, что  является сферой радиуса r с центром в начале координат; точки
является сферой радиуса r с центром в начале координат; точки  R3, для которых
R3, для которых  , образуют коническую поверхность с осью OZ; при
, образуют коническую поверхность с осью OZ; при  имеем полуплоскость, исходящую из оси OZ.
имеем полуплоскость, исходящую из оси OZ.
 Пример. Вычислим тройной интеграл
Пример. Вычислим тройной интеграл  , если тело Q ограничено сферой
, если тело Q ограничено сферой  (см. Рис. 5).
(см. Рис. 5).
à z Переходя к сферическим координатам и используя



 формулу (6), будем иметь:
формулу (6), будем иметь:




 y
y
x Рис. 5


 R3. Сферические координаты точки М - числа r, q, j, где r – расстояние от точки M до начала координат (длина радиуса-вектора
R3. Сферические координаты точки М - числа r, q, j, где r – расстояние от точки M до начала координат (длина радиуса-вектора  ), q - величина угла (в радианах), образованного лучом OM с положительным направлением оси OZ, а j - величина угла, образованного лучом OP (P – проекция точки M на плоскость OXY) с положительным направлением оси OX ( см. Рис.4).
), q - величина угла (в радианах), образованного лучом OM с положительным направлением оси OZ, а j - величина угла, образованного лучом OP (P – проекция точки M на плоскость OXY) с положительным направлением оси OX ( см. Рис.4). для
для 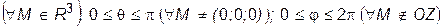
 z
z

 M
M q r Z
q r Z



 0 y y
0 y y j
j
 x P
x P . (5)
. (5)
 .
. . (6)
. (6) или когда область интегрирования есть шар
или когда область интегрирования есть шар  .
. является сферой радиуса r с центром в начале координат; точки
является сферой радиуса r с центром в начале координат; точки  , образуют коническую поверхность с осью OZ; при
, образуют коническую поверхность с осью OZ; при  имеем полуплоскость, исходящую из оси OZ.
имеем полуплоскость, исходящую из оси OZ. , если тело Q ограничено сферой
, если тело Q ограничено сферой  (см. Рис. 5).
(см. Рис. 5).
 формулу (6), будем иметь:
формулу (6), будем иметь:



 y
y



