Центры масс (центры тяжести фигур)
I. Статические моменты и центр тяжести плоской материальной фигуры Определение 1. Пусть в R 2 относительно заданной декартовой системы координат OXY дана материальная точка (x;y) массы m. Статическим моментом точки (x;y) относительно оси Ox (Oy) называется произведение массы этой точки на ее ординату (абсциссу):
Определение 2. Статическим моментом относительно оси Ox (Oy) системы конечного числа материальных точек
Пусть теперь в R2 относительно прямоугольной системы координат OXY дана материальная фигура D с поверхностной плотностью
Возьмем произвольное разбиение T фигуры
Определение 3. Если при
Так как плотность
Определение 4. Точка
Из формул (2) и (5¢) получаем
. Если фигура D однородная, т.е.
где Пример 1. Найдем координаты центра тяжести однородной фигуры D, ограниченной линиями à Так как данная материальная однородная фигура D симметрична относительно оси OX, то
-1 0 2 x
Рис. 1 Имеем:
Следовательно, Таким образом, точка
II. Статические моменты и центр тяжести пространственного тела Пусть в R3 дотносительно заданной декартовой системы координат OXYZ дано материальное тело Q с объемной плотностью
где III. Моменты инерции плоской материальной фигуры относительно данной прямой или точки Определение. Моментом инерции материальной точки A массы m относительно данной прямой (точки) называется произведение массы этой точки А на квадрат ее расстояния до этой прямой (точки):
По аналогии с рассуждениями п.I, вводятся понятия моментов инерции ситемы конечного числа материальных точек относительно данной прямой l материальной фигуры DÌR2 с поверхностной плотностью
В частности, моменты инерции фигуры D относительно осей OX и OY соответственно равны:
а момент инерции этой фигуры относительно начала координат выражается формулой
Предполагается, что в приведенных формулах плотность Заметим, что
В случае пространственного материального тела Для момента инерции этого тела относительно координатных плоскостей, координатных осей и начала координат, имеют место формулы:
Упражнения 1. Определите массу пирамиды, образованной плоскостями 2. Найдите массу вещества, заполняющего общую часть двух шаров 3. Найдите центр тяжести: 1) однородного тела, ограниченного поверхностями
2) полушара 4. Неоднородное тело ограничено плоскостями [n1]
|


 , имеющих массы
, имеющих массы  называется сумма статических моментов этих точек относительно оси Ox (Oy):
называется сумма статических моментов этих точек относительно оси Ox (Oy): (1)
(1) . Будем предполагать, что D – связной простой компакт, а функция
. Будем предполагать, что D – связной простой компакт, а функция  . (2)
. (2) D на любое конечное число n квадрируемых ячеек
D на любое конечное число n квадрируемых ячеек  попарно без общих внутренних точек. Площади ячеек
попарно без общих внутренних точек. Площади ячеек  обозначим через
обозначим через  . В каждой ячейке
. В каждой ячейке 
 ячейки
ячейки  . Если диаметр
. Если диаметр  разбиения T достаточно мал, то можно считать, что эта масса сосредоточена в точке
разбиения T достаточно мал, то можно считать, что эта масса сосредоточена в точке 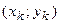 . Введем в рассмотрение следующие суммы, составленные по закону (1):
. Введем в рассмотрение следующие суммы, составленные по закону (1): (3)
(3) существует конечный предел суммы
существует конечный предел суммы  (
( ), то он называется статическим моментом материальной фигуры D относительно оси Ox (Oy):
), то он называется статическим моментом материальной фигуры D относительно оси Ox (Oy): . (4)
. (4) по предположению непрерывна в D, а суммы (3) – это интегральные суммы для непрерывных в D функций
по предположению непрерывна в D, а суммы (3) – это интегральные суммы для непрерывных в D функций  и
и  , то указанные пределы существуют, причем
, то указанные пределы существуют, причем . (5)
. (5) с сосредоточенной в ней массой (2) материальной фигуры D
с сосредоточенной в ней массой (2) материальной фигуры D  R2 называется центром тяжести (центром масс) фигуры D, если статические моменты этой материальной точки относительно осей Ox и Oy равны соответственно статическим моментам фигуры D относительно этих осей, т.е. если
R2 называется центром тяжести (центром масс) фигуры D, если статические моменты этой материальной точки относительно осей Ox и Oy равны соответственно статическим моментам фигуры D относительно этих осей, т.е. если . (5¢)
. (5¢) (6)
(6) , то формулы (6) упрощаются:
, то формулы (6) упрощаются: , (7)
, (7)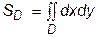 - площадь фигуры D.
- площадь фигуры D. (см. Рис. 1).
(см. Рис. 1). . Для нахождения
. Для нахождения  воспользуемся первой из формул (7).
воспользуемся первой из формул (7). y
y




 2
2


 -2
-2



 - центр тяжести данной фигуры D. ¨
- центр тяжести данной фигуры D. ¨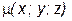 (будем считать, что функция
(будем считать, что функция  непрерывна в Q). По аналогии с плоским случаем вводятся понятия статических моментов
непрерывна в Q). По аналогии с плоским случаем вводятся понятия статических моментов  тела Q относительно координатных плоскостей, а также центра тяжести этого тела. При этом имеют место формулы:
тела Q относительно координатных плоскостей, а также центра тяжести этого тела. При этом имеют место формулы:


 .
. .
. .
.

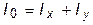 .
. R3 (с объемной плотностью
R3 (с объемной плотностью 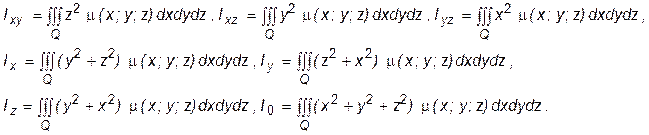
 если плотность в каждой ее точке пропорциональна аппликате этой точки.
если плотность в каждой ее точке пропорциональна аппликате этой точки. и
и  , если его плотность в каждой точке пропорциональна расстоянию ее до плоскости OXY.
, если его плотность в каждой точке пропорциональна расстоянию ее до плоскости OXY.
 , у которого объемная плотность в каждой точке численно равна расстоянию от этой точки до центра его основания.
, у которого объемная плотность в каждой точке численно равна расстоянию от этой точки до центра его основания. и цилиндром
и цилиндром 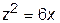 . Объемная плотность вещества в каждой его точке пропорциональна ее расстоянию от плоскости OXY. Найдите момент инерции этого тела относительно оси OZ.
. Объемная плотность вещества в каждой его точке пропорциональна ее расстоянию от плоскости OXY. Найдите момент инерции этого тела относительно оси OZ.


