II. Двойной интеграл в полярных координатах
Пусть x, y – декартовы координаты точки PÎD, а r и j - полярные координаты этой точки, так что:
Якобиан отображения (10) равен r
Компакт D будем называть правильным в направлении лучей y
j=j2 r=F2(j)
j=j1 j2 r=F1(j) j1 0 x Рис.5
Далее, пусть компакт D ограничен лучами Формула (8) примет вид:
Если полюс О принадлежит компакту D, то Пример 1. Вычислим двойной интеграл
à Компакт D является образом компакта (прямоугольника)
якобиан которого равен r.
1
0 1
Рис.6 Поэтому, переходя от декартовых координат к полярным, согласно формуле (11) будем иметь:
Пример 2. Вычислим двойной интеграл
где
à Область интегрирования D есть замкнутый круг радиуса
Рис. 7 будем иметь:
|
. (10)
.
, если любой луч, выходящий из начала координат и проходящий через внутреннюю точку P компакта D, пересекает границу этого компакта в двух точках P1 и P2. При этом точка P1 называется точкой входа этого луча в компакт D, а точка P2 – точкой выхода этого луча из D.
y
P2
P1
и линиями r=F2(j) и r=F1(j), состоящими соответственно из точек входа и точек выхода. (см. Рис. 5)
или
. (11)
.
, где 
R2 
.
при отображении:
,
j
y
p
D*
-1 0 1 x
,
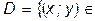R2 
.
с центром в точке 
поскольку
. 
y
Переходя к полярным координатам и учитывая, что при
любом фиксированном 
0 1 x изменяется (в пределах области) от 0 до cosj (так как
,
