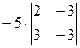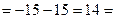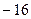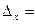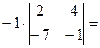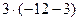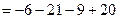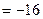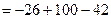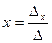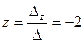Обратная матрица
Определение 11. Квадратная матрица (т = п) называется вырожденной, если ее определитель равен нулю, и невырожденной в противном случае. Определение 12. Если А - невырожденная матрица, то существует, и притом единственная, матрица
где Е - единичная матрица того же размера, что и матрицы А и А-1. Матрица А-1 называется обратной к матрице А. Определение 13. Назовем матрицу АT транспонированной, если она является транспонированной матрицей, составленной из алгебраических дополнений соответствующих элементов матрицы А. Если матрица А — невырожденная, то
Пример 2. Вычислить матрицу 2А+ 5В, если
Решение.
Ответ Пример 3. Даны матрицы
Ответ: Замечание. Очевидно, АВ≠ ВА, т.е. произведение матриц не перестановочно. Пример 4. Доказать, что матрица является обратной для матрицы Решение.
Ответ: матрица А-1 является обратной матрице А. Пример 5. Найти транспонируемую матрицу для матрицы
Решение. Присоединенная матрица является транспонированной матрицей из алгебраических дополнений данной матрицы.
Для данной матрицы
Итак, транспонируемая матрица АТ равна
Пример 6. Найти матрицу А-1, обратную к матрице А примера 5. Решение. Так как
Тема 1.2 Системы линейных уравнений Решить систему линейных неоднородных алгебраических уравнений.
|

 такая, что
такая, что ,
,


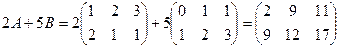

 Найти матрицы АВ и ВА.
Найти матрицы АВ и ВА.
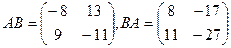

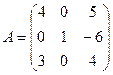


 -
-


 , то найдем
, то найдем