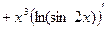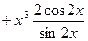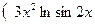Производная неявной функции.
Если функции то для нахождения производной
Пример 1. Найти вторую производную Решение. Дифференцируя по
Равенство (*) снова продифференцируем по
Пример 2. Найти значение заданной неявно, если
Решение.
Подставим
Параметрическое дифференцирование:
Пример: Дана функция Найти Решение.
Пример. Найти производную Решение: Используем правило
Логарифмическое дифференцирование Рассмотрим метод нахождения производной степенно-показательной функции
Пример. Найти производную функции Решение.
Раскрытие неопределенностей
|
задана уравнением, не разрешенным относительно 
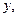
надо продифференцировать по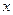 
обе части этого уравнения, учитывая, что 
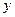есть функция по 
и затем разрешить полученное уравнение относительно 
Чтобы найти 
надо уравнение продифференцировать дважды по 
от функции 
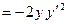
для функции 
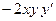
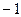
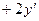
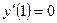
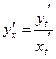
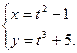
, если функция задана параметрически: 
.
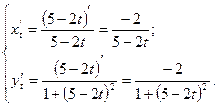
, у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию: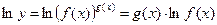 
. Теперь продифференцируем обе части полученного равенства: 
.Отсюда 
.
