- Даны вершины треугольника ABC: A (-2, 4), В (3, 1), С (10, 7).Найти: а) уравнение стороны АВ; б) уравнение высоты CH; в) уравнение медианы АМ; г) уравнение прямой, проходящей через вершину С параллельно стороне АВ.
- Записать уравнение прямой, проходящей через точку A(3, 1) перпендикулярно к прямой BC, если В(2, 5), С(1, 0).
- Найти точку O пересечения диагоналей четырехугольника ABCD, если A(-1, -3), B(3, 5), С(5,2), D(3,-5).
- Найти уравнение стороны АВ треугольника АВС, если А(-3;-2), В(14;4), С(6;8)
- Дан треугольник c вершинами А(3, 1), В(-3, -1) и С(5, -12). Найти уравнение и вычислить длину его медианы, проведенной из вершины С.
6. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2y - x = 3.
- Доказать, что четырехугольник ABCD - трапеция, если A(3, 6), В(5, 2), С(-1, -3), D(-5, 5).
- Треугольник задан вершинами А(2; -1), В(-7, 3) и С(-1, -5). Составить уравнение биссектрисы угла С.
ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Теория пределов. Непрерывность
Бесконечно малые и бесконечно большие величины. Связь между ними.
Если  бесконечно большая величина, то обратная ей величина -
бесконечно большая величина, то обратная ей величина -  бесконечно малая.
бесконечно малая.  Если
Если  бесконечно малая величина, то обратная ей величина -
бесконечно малая величина, то обратная ей величина - 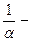 бесконечно большая.
бесконечно большая.


Понятие предела функции.
Число  называется пределом функции
называется пределом функции  в точке
в точке  , если для всех
, если для всех 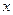 , достаточно близких к
, достаточно близких к  и отличных от
и отличных от  , значения функции
, значения функции  сколь угодно мало отличаются от числа
сколь угодно мало отличаются от числа  .
.

 бесконечно большая величина, то обратная ей величина -
бесконечно большая величина, то обратная ей величина -  бесконечно малая.
бесконечно малая.  Если
Если  бесконечно малая величина, то обратная ей величина -
бесконечно малая величина, то обратная ей величина - 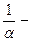 бесконечно большая.
бесконечно большая. называется пределом функции
называется пределом функции  в точке
в точке  , если для всех
, если для всех 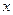 , достаточно близких к
, достаточно близких к 


