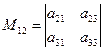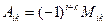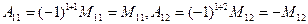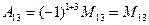Определители второго порядка.
Практикум
для студентов специальностей 260301, 260302, 260303, 260501, 260505, 260100,240901, 240902, 200503, 110501, 110502, 111201, 240502, 261201
Редактор И.А.Мырсина
Подписано в печать 14.01.09. Усл. печ. л. 7,3. Тираж экз. Заказ. Изд. №. МГУПБ. 109316, Москва, ул. Талалихина, 33. ООО «Полисувенир», 109316. Москва, ул. Талалихина, 33. Тел. 677-03-86
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Матрицы и определители Определители второго порядка. Определение 1. Матрицей размера 2x2 называется совокупность чисел, расположенных в виде таблицы из 2 строк и 2 столбцов. Обозначается Числа, составляющие Определение 2. Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число Определитель обозначают символом
По определению, Числа а11, а12, а21, а22 называются элементами определителя.
Определение 3. Если
(3 строки, 3 столбца), то соответствующим ей определителем третьего порядка называется число, которое вычисляется следующим образом
Числа а11, а12,..., а33 называются элементами определителя. Формула дает разложение определителя третьего порядка по элементам первой строки и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка. Определение 4. Назовем минором, соответствующим данному элементу определителя третьего порядка, определитель второго порядка, полученный из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Миноры будем обозначать заглавной буквой М с двумя индексами. Так, например, минор М12, соответствующий элементу а12, есть определитель Определение 5. Назовем алгебраическим дополнением элемента определителя его минор, взятый со знаком плюс, если сумма номеров строки и столбца, в которых стоит элемент, четна, и со знаком минус, если эта сумма нечетна. Алгебраическое дополнение элемента aik обозначается через Aik. Здесь i означает номер строки, а к - номер столбца, на пересечении которых находится данный элемент.
Например,
|

 эту матрицу, называются ее элементами и обозначаются буквой с двумя индексами. Первый индекс указывает номер строки, а второй - номер столбца, в которых стоит данное число.
эту матрицу, называются ее элементами и обозначаются буквой с двумя индексами. Первый индекс указывает номер строки, а второй - номер столбца, в которых стоит данное число.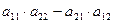 .
.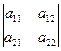
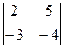


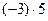
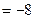


 - квадратная матрица размера 3x3
- квадратная матрица размера 3x3