ОСНОВНЫЕ ПОНЯТИЯ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
1. Векторы в пространстве. В пространстве, как и на плоскости, вектором называется направленный отрезок. Векторы, расположенные на прямых, параллельных одной и той же плоскости, или лежащие в этой плоскости, называются компланарными. Три вектора, среди которых имеется хотя бы один нулевой вектор, считаются компланарными. Любой вектор
2. Прямоугольная система координат в пространстве. Пусть в пространстве задана тройка попарно перпендикулярных единичных векторов Разложение вектора
Если началом вектора
и записывается в виде
3. Правила действий над векторами, заданными своими координатами. Если в базисе координаты разности двух векторов равны:
координаты произведения вектора на число:
4. Условие коллинеарности двух векторов. Условие коллинеарности двух векторов
Если
5. Длина вектора. Длина вектора
Длина радиус-вектора
6. Деление отрезка в данном отношении. Если отрезок АВ разделен точкой С в отношении
При
7. Направляющие косинусы вектора. Углы, образуемые радиус-вектором
Косинусы углов, вычисляемые по этим формулам, называются направляющими косинусами вектора Для направляющих косинусов вектора имеет место соотношение
|

 пространства можно разложить по трем заданным некомпланарным векторам
пространства можно разложить по трем заданным некомпланарным векторам  :
:
 , отложенных от некоторого начала — точки О. Такую тройку векторов называют прямоугольным базисом в пространстве. Совокупность начала О и прямоугольного базиса
, отложенных от некоторого начала — точки О. Такую тройку векторов называют прямоугольным базисом в пространстве. Совокупность начала О и прямоугольного базиса  называют прямоугольной системой координат в пространстве.
называют прямоугольной системой координат в пространстве. в базисе
в базисе 
 концом — точка
концом — точка 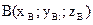 , то вектор
, то вектор  имеет координаты, равные разностям соответствующих координат точек B и A:
имеет координаты, равные разностям соответствующих координат точек B и A:

 и
и  , то:
, то:  ;
; ;
;

 , то векторы
, то векторы  имеют одинаковое направление; если т<0, то направления векторов противоположны.
имеют одинаковое направление; если т<0, то направления векторов противоположны.

 , то координаты точки С находятся по формулам
, то координаты точки С находятся по формулам
 получаются формулы для нахождения координат середины отрезка:
получаются формулы для нахождения координат середины отрезка:
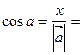





 .
.


