Пример 1. Исследовать функцию на непрерывность.Исследовать функцию на непрерывность.
Решение. Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точках x = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.
Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода.
Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода.
Пример 2 Найти точки разрыва функции
Вычислим односторонние пределы при x = 0.
Первый замечательный предел.
Примеры.
Второй замечательный предел.
Примеры.
Функция α (x) называется бесконечно малой при x®a, если
Предположим, что α (x) и β (x) - бесконечно малые функции при x®a.
Если
то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);
Если, то говорят, что функции α (x) и β (x)
являются бесконечно малыми одинакового порядка малости;
Если,то говорят, что функция α (x) является бесконечно малой порядка n относительно функции β (x);
Если,то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при x®a
Таблица эквивалентных функций
Доказать, что функции
Решение.
|
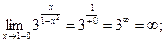
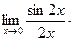
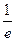
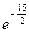
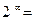
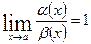
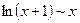
и 
при 
являются бесконечно малыми одного порядка малости.
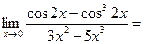
данные функции – бесконечно малые одного порядка малости.
