Теорема: Если вторая производная функции в данном промежутке положительна, то кривая вогнута в этом промежутке, а если отрицательна – выпукла в этом промежутке.
Пример. Найти интервалы выпуклости и вогнутости и точки перегиба кривой Решение:
Точка перегиба
Задача. Найти наибольшее и наименьшее значения функции Решение:
Точка 3. Вычислим значения функции в точках 0, 5, 6: y(0)=225, y(5)=50, y(6)=63. Ответ: Метод поиска наибольших и наименьших значений функции применим к решению разнообразных прикладных задач. Задача. Число 15 представить в виде суммы двух положительных слагаемых так, чтобы произведение квадрата первого из них на второе было наибольшим. Решение: Пусть первое число х, тогда второе – (15-х). Составим функцию
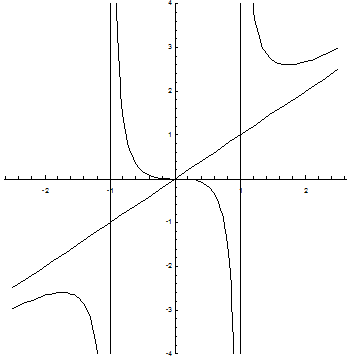
Произведение квадрата первого числа на второе будет наибольшим, если одно из чисел 10, а другое будет 5 . Пример. Исследовать функцию
1. D(y)= 2.E(y)= 3. 4. 5. Найдем наклонные асимптоты.
6.
Критические точки:
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < - - -1 < x < 0, y¢ < 0, функция убывает 0 < x < 1, y¢ < 0, функция убывает 1 < x <
7.
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < - - -1 < x < 0, y¢¢ > 0, кривая вогнутая 0 < x < 1, y¢¢ < 0, кривая выпуклая 1 < x <
Видно, что точка х = -
|

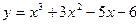
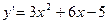


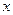

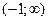


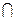
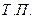
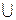
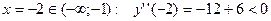
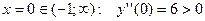
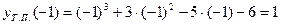

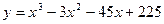 на отрезке
на отрезке 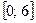


 ее из рассмотрения исключаем.
ее из рассмотрения исключаем.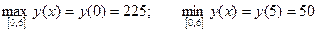

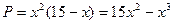
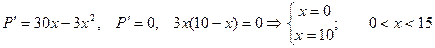
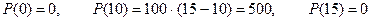
 и построить ее график.
и построить ее график.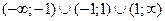
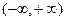
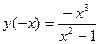 - функция нечетная, график симметричен относительно начала координат, непериодичная
- функция нечетная, график симметричен относительно начала координат, непериодичная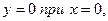

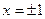 - вертикальные асимптоты
- вертикальные асимптоты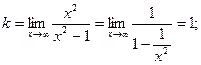
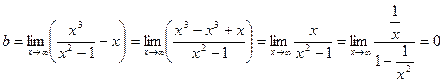
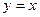 - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты.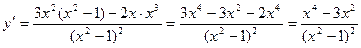
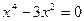
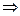
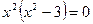
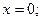
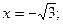


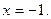
 , y¢ > 0, функция возрастает
, y¢ > 0, функция возрастает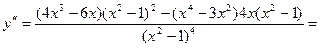

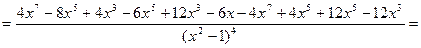
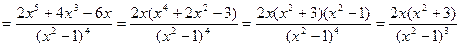 .
.