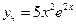y''+ρx+qy=f(x),
где f(x) – непрерывная функция, отличная от нуля.
Общее решение такого уравнения представляет собой сумму частного решения и общего решения y0
Рассмотрим различные виды правых частей уравнения (3).
1. Характеристическое уравнение имеет два различных действительных корня, отличных от нуля
Пример. Рассмотрим неоднородное уравнение 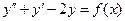 Для соответствующего однородного уравнения составим характеристическое уравнение
Для соответствующего однородного уравнения составим характеристическое уравнение 
|
Правая часть 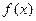
| В каком виде нужно искать частное решение 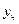 неоднородного уравнения неоднородного уравнения
|
1.  ) )
| 
|
2. 
| 
|
3. 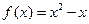
| 
|
4. 
| 
|
Примечание. Обратите внимание, когда в правой части находится неполный многочлен, то частное решение подбирается без пропусков степеней, пример:  . Это многочлен первой степени, и в нем отсутствует константа. Однако при подборе частного решения константу пропускать нельзя, т.е. частное речение нужно искать в виде: . Это многочлен первой степени, и в нем отсутствует константа. Однако при подборе частного решения константу пропускать нельзя, т.е. частное речение нужно искать в виде: 
|
5. 
| Коэффициент в показателе экспоненты:  не совпадает с корнем характеристического уравнения не совпадает с корнем характеристического уравнения  Поэтому частное решение ищем в виде: Поэтому частное решение ищем в виде: 
|
6. 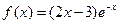
| Коэффициент в показателе экспоненты: 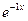 не совпадает с корнем характеристического уравнения не совпадает с корнем характеристического уравнения  . Поэтому частное решение ищем в виде: . Поэтому частное решение ищем в виде: 
|
7. 
| Коэффициент в показателе экспоненты:  совпадает с корнем характеристического уравнения совпадает с корнем характеристического уравнения  Поэтому частное решение Поэтому частное решение  нужно домножить на х, т.е. искать в виде: нужно домножить на х, т.е. искать в виде:  , получим , получим 
|
8. 
| Коэффициент в показателе экспоненты:  совпадает с корнем характеристического уравнения совпадает с корнем характеристического уравнения  . Поэтому частное решение . Поэтому частное решение  домножаем на х, т.е. ищем в виде домножаем на х, т.е. ищем в виде 
|
Примечание. В случае неполных многочленов степени не теряются, например, если  (в многочлене отсутствует (в многочлене отсутствует  и константа), то частное решение следует искать в виде: и константа), то частное решение следует искать в виде:  . Если . Если  (в многочлене отсутствует х в первой степени), то частное решение ищем в виде: (в многочлене отсутствует х в первой степени), то частное решение ищем в виде: 
|
9. 
| 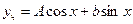
|
10. 
| 
|
11. 
| 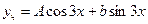
|
Примечание. В подборе частного решения всегда должен присутствовать и синус и косинус (даже, если в правую часть 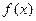 входит только синус или только косинус) входит только синус или только косинус)
|
-
 | 
|
-
 | 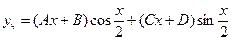
|
-
 | 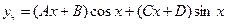
|
|
|
|
| | | | | |
ПРИМЕР 1.
Решить дифференциальное уравнение: 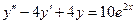
Решение записывается в виде: 

1) Найдем общее решение:  , составим характеристическое уравнение:
, составим характеристическое уравнение:
 ,тогда общее решение находится по формуле:
,тогда общее решение находится по формуле: 
2) Найдем частное решение:  , тогда частное решение находится по формуле (см. таблицу)
, тогда частное решение находится по формуле (см. таблицу) 


Подставим в исходное уравнение



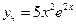
Тогда решение запишется в виде: 

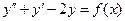 Для соответствующего однородного уравнения составим характеристическое уравнение
Для соответствующего однородного уравнения составим характеристическое уравнение 
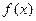
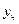 неоднородного уравнения
неоднородного уравнения
 )
)



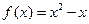



 . Это многочлен первой степени, и в нем отсутствует константа. Однако при подборе частного решения константу пропускать нельзя, т.е. частное речение нужно искать в виде:
. Это многочлен первой степени, и в нем отсутствует константа. Однако при подборе частного решения константу пропускать нельзя, т.е. частное речение нужно искать в виде: 
 не совпадает с корнем характеристического уравнения
не совпадает с корнем характеристического уравнения  Поэтому частное решение ищем в виде:
Поэтому частное решение ищем в виде: 
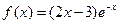
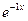 не совпадает с корнем характеристического уравнения
не совпадает с корнем характеристического уравнения 

 совпадает с корнем характеристического уравнения
совпадает с корнем характеристического уравнения  Поэтому частное решение
Поэтому частное решение  нужно домножить на х, т.е. искать в виде:
нужно домножить на х, т.е. искать в виде:  , получим
, получим 

 совпадает с корнем характеристического уравнения
совпадает с корнем характеристического уравнения  . Поэтому частное решение
. Поэтому частное решение  домножаем на х, т.е. ищем в виде
домножаем на х, т.е. ищем в виде 
 (в многочлене отсутствует
(в многочлене отсутствует  и константа), то частное решение следует искать в виде:
и константа), то частное решение следует искать в виде:  . Если
. Если  (в многочлене отсутствует х в первой степени), то частное решение ищем в виде:
(в многочлене отсутствует х в первой степени), то частное решение ищем в виде: 

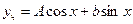



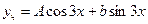



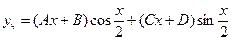

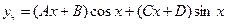
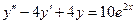


 , составим характеристическое уравнение:
, составим характеристическое уравнение: ,тогда общее решение находится по формуле:
,тогда общее решение находится по формуле: 
 , тогда частное решение находится по формуле (см. таблицу)
, тогда частное решение находится по формуле (см. таблицу)