Радикальный признак Коши.
Если для ряда
Пример. С помощью радикального признака Коши исследовать сходимость рядов:
Решение:
Решение:
Интегральный признак Коши. Пусть Пример.
Решение. Общий член ряда
Решение.
Знакочередующиеся ряды. Признак сходимости Лейбница. Знакочередующимся рядом называется ряд вида
Признак Лейбница (достаточный признак сходимости знакочередующихся рядов). Если члены ряда (1) начиная с некоторого монотонно убывают по абсолютной величине и Пример. Исследовать ряд на сходимость по признаку Лейбница:
Решение. Так как члены данного ряда по абсолютной величине монотонно убывают:
Абсолютная и условная сходимость знакопеременного ряда.
Ряд
|
существует предел 
то при 
ряд сходится, при 
ряд расходится, при 
вопрос о сходимости остается открытым.
данный ряд сходится.
ряд расходится.
непрерывная, положительная и монотонно убывающая функция, определенная при 
Тогда ряд 
сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл 
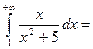
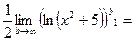
значит данный ряд расходится.
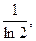данный ряд сходится.
(1) где 
положительные числа.
, то ряд (1) сходится.
и общий член при 
стремится к нулю: 
то в силу признака Лейбница ряд сходится.
(1) называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
