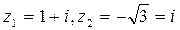Упражнения к экзаменам
Задание 1 Выполнить действия над комплексными числами, заданными в алгебраической форме и результат изобразить геометрически: a) Задание 2 Произвести действие и результат представить в тригонометрической форме: a)
Задание 3 Представить в тригонометрической и показательной форме число: a) Задание 4 Найти модуль и аргумент комплексного числа: a) z =1- i b) z = -3 +3 i c) Задание 5 Вычислите: a) Задание 6 Извлеките корень: a)
Задание 7 Выполнить действия и записать ответ в тригонометрической и показательной формах: Задание 8 Выполнить следующие действия над комплексными числами: Задание 9 Дано: Вычислить:
Вопросы к экзаменам
По дисциплине Математика для специальностей 230115 заочного отделения 3 курса
1. Определители второго и третьего порядка, их вычисление и свойства. 2. Определители n-го порядка, их вычисление. 3. Теорема о разложении определителя по элементам любой строки или столбца. 4. Миноры и алгебраические дополнения. 5. Матрицы, действия над ними. 6. Обратная матрица, алгоритм нахождения. 7. Решение систем линейных уравнений с двумя и тремя неизвестными при помощи определителей (по формулам Крамера) 8. Решение систем линейных уравнений методом Гаусса. 9. Матричный способ решения систем. 10. Векторы, линейные операции над ними. 11. Декартовы прямоугольные координаты в пространстве. Координаты вектора. 12. Скалярное произведение векторов. 13. Векторное произведение векторов. 14. Смешанное произведение векторов. 15. Общее уравнение прямой, его частные случаи. 16. Угловой коэффициент прямой. Уравнение прямой с угловым коэффициентом и начальной ординатой. 17. Уравнение прямой в отрезках. 18. Уравнение прямой, проходящей через две точки. 19. Уравнение прямой, проходящей через точку в данном направлении (уравнение пучка прямых). 20. Взаимное расположение двух прямых. Условие параллельности и перпендикулярности прямых. 21. Расстояние от точки до прямой. 22. Угол между прямыми. 23. Окружность, ее уравнения. 24. Эллипс, его уравнение. 25. Гипербола, ее уравнение. 26. Парабола, ее уравнение. 27. Бесконечно малые и бесконечно большие функции. 28. Понятие предела функции. 29. Техника вычисления пределов. Раскрытие неопределенностей. 30. Сравнение бесконечно малых. Принцип замены эквивалентными. 31. Приращение аргумента и приращение функции. 32. Непрерывность и точки разрыва функции. 33. Понятие производной. Правило нахождения. 34. Основные правила дифференцирования. Дифференцирование основных элементарных функций. 35. Дифференцирование сложной функции. 36. Производные высших порядков. 37. Производная неявной функции. 38. Логарифмическое дифференцирование. 39. Геометрические приложения производной. 40. Механические приложения производной. 41. Дифференциал функции 42. Раскрытие неопределенностей. Правило Лопиталя. 43. Промежутки монотонности функции. 44. Экстремумы функции. 45. Наименьшее и наибольшее значения функции. 46. Выпуклость и вогнутость кривой. Точки перегиба. 47. Асимптоты. Алгоритм нахождения. 48. Неопределенный интеграл и его свойства. 49. Непосредственное интегрирование. 50. Интегрирование способом подстановки. Алгоритм. 51. Интегрирование по частям. 52. Интегрирование функций, содержащих квадратный трехчлен. 53. Интегрирование рациональных дробей. 54. Интегрирование тригонометрических функций. 55. Интегрирование простейших иррациональных функций. 56. Определенный интеграл и его свойства. 57. Методы интегрирования определенного интеграла. 58. Приложения определенного интеграла (вычисление площадей плоской фигуры, решение физических задач. 59. Числовые ряды. Основные понятия. 60. Необходимый и достаточные признаки сходимости положительных рядов. 61. Знакочередующиеся ряды. Признак сходимости Лейбница. 62. Степенные ряды. 63. Разложение элементарных функций в степенные ряды. 64. Приложение рядов к приближенным вычислениям. 65. Дифференциальные уравнения. Основные понятия и определения. 66. Уравнения с разделяющимися переменными. Алгоритм решения. 67. Однородные уравнения. 68. Линейные уравнения. Алгоритм решения. 69. Линейные однородные дифференциальные уравнения второго порядка. Алгоритм решения. 70. Понятие комплексного числа. Степени мнимой единицы. 71. Алгебраическая форма комплексного числа. Действия в ней. 72. Тригонометрическая форма комплексного числа. Действия в ней. 73. Показательная форма комплексного числа. Действия в ней. 74. Перевод из одной формы комплексного числа в другую.
|

 b)
b) 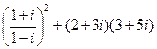 c)
c) 
 b)
b)  c)
c) 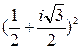
 b)
b)  c) z = 5 + 5 i
c) z = 5 + 5 i
 b)
b)  c)
c) 
 b)
b)  c)
c) 
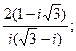
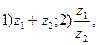 если
если