1) Определения и общие замечания. Интервал сходимости.
Ряд вида
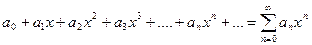
называется степенным рядом.
Числа  называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда.
Придавая x различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений x, при которых ряд сходится, называется областью его сходимости.
Очевидно, что частичная сумма степенного ряда  является функцией переменной x. Поэтому и сумма ряда S также является некоторой функции её переменной x, определённой в области сходимости ряда:
является функцией переменной x. Поэтому и сумма ряда S также является некоторой функции её переменной x, определённой в области сходимости ряда:  (или
(или  ). Число R называется радиусом сходимости ряда, если при
). Число R называется радиусом сходимости ряда, если при  ряд сходится, а при
ряд сходится, а при  - расходится. Интервал (-R,R) в этом случае называется интервалом сходимости ряда. Если ряд сходится на всей числовой прямой, то пишут R=∞; если он сходится только при x=0, то пишут R=0.
- расходится. Интервал (-R,R) в этом случае называется интервалом сходимости ряда. Если ряд сходится на всей числовой прямой, то пишут R=∞; если он сходится только при x=0, то пишут R=0.
При x=  может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.
может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.
Радиус сходимости можно найти по формуле  , если соответствующий предел существует.
, если соответствующий предел существует.
Пример. Рассмотрим ряд
 Это степенной ряд, все коэффициенты его, за исключением
Это степенной ряд, все коэффициенты его, за исключением  , отличные от нуля. Найдем радиус и интервал сходимости данного ряда. Здесь
, отличные от нуля. Найдем радиус и интервал сходимости данного ряда. Здесь  и
и  . Поэтому
. Поэтому 
Следовательно, радиус сходимости R=1 и ряд сходится на интервале (-1,1). Исследуем поведение ряда на концах интервала сходимости т.е. в точках x=  . При x=1получаем гармонический ряд
. При x=1получаем гармонический ряд  , а при x=-1 – ряд
, а при x=-1 – ряд  , который сходится в силу признака Лейбница. Таким образом данный ряд сходится в любой точке полуинтервала [-1,1) и расходитя вне его.
, который сходится в силу признака Лейбница. Таким образом данный ряд сходится в любой точке полуинтервала [-1,1) и расходитя вне его.
2) Разложение функций в степенные ряды. Если функция  на интервале (-R,R) разлагается в степенной ряд
на интервале (-R,R) разлагается в степенной ряд 

 то коэффициенты этого ряда определяются по формулам
то коэффициенты этого ряда определяются по формулам
 ,
,  подставляя выражения коэффициентов в равенство, получаем
подставляя выражения коэффициентов в равенство, получаем 
Ряд стоящий в правой части формулы, называется рядом Маклорена для функции  .
.
При разложении функции в степенные ряды часто используются разложения в ряд Маклорена следующих функций:

 ;
;







 .
.
Где а –любое вещественное число.

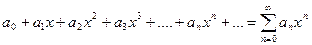
 называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда. является функцией переменной x. Поэтому и сумма ряда S также является некоторой функции её переменной x, определённой в области сходимости ряда:
является функцией переменной x. Поэтому и сумма ряда S также является некоторой функции её переменной x, определённой в области сходимости ряда:  (или
(или  ). Число R называется радиусом сходимости ряда, если при
). Число R называется радиусом сходимости ряда, если при  ряд сходится, а при
ряд сходится, а при  - расходится. Интервал (-R,R) в этом случае называется интервалом сходимости ряда. Если ряд сходится на всей числовой прямой, то пишут R=∞; если он сходится только при x=0, то пишут R=0.
- расходится. Интервал (-R,R) в этом случае называется интервалом сходимости ряда. Если ряд сходится на всей числовой прямой, то пишут R=∞; если он сходится только при x=0, то пишут R=0. может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.
может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда. , если соответствующий предел существует.
, если соответствующий предел существует. Это степенной ряд, все коэффициенты его, за исключением
Это степенной ряд, все коэффициенты его, за исключением  , отличные от нуля. Найдем радиус и интервал сходимости данного ряда. Здесь
, отличные от нуля. Найдем радиус и интервал сходимости данного ряда. Здесь  и
и  . Поэтому
. Поэтому 
 . При x=1получаем гармонический ряд
. При x=1получаем гармонический ряд  , а при x=-1 – ряд
, а при x=-1 – ряд  , который сходится в силу признака Лейбница. Таким образом данный ряд сходится в любой точке полуинтервала [-1,1) и расходитя вне его.
, который сходится в силу признака Лейбница. Таким образом данный ряд сходится в любой точке полуинтервала [-1,1) и расходитя вне его. на интервале (-R,R) разлагается в степенной ряд
на интервале (-R,R) разлагается в степенной ряд 

 то коэффициенты этого ряда определяются по формулам
то коэффициенты этого ряда определяются по формулам ,
,  подставляя выражения коэффициентов в равенство, получаем
подставляя выражения коэффициентов в равенство, получаем 

 ;
;







