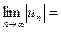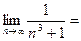Признак сходимости знакопеременного ряда
Если ряд
Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд (2), составленный из абсолютных величин членов данного ряда (1). Сходящийся знакопеременный ряд называется условно сходящимся, если ряд, составленный из абсолютных величин его членов, расходится. Пример. Исследовать на абсолютную и условную сходимость ряды:
Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: По признаку Даламбера этот ряд сходится, так как
Решение. Исследуем ряд
Решение. Согласно признаку Лейбница ряд сходится: Ряд из абсолютных величин его членов Значит данный ряд условно сходящийся.
Решение. По признаку Лейбница ряд сходится:
|

 составленный из абсолютных величин членов ряда (1) сходится, то ряд (1) также сходится.
составленный из абсолютных величин членов ряда (1) сходится, то ряд (1) также сходится.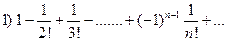


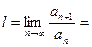



 таким образом, исследуемый ряд является абсолютно сходящимся.
таким образом, исследуемый ряд является абсолютно сходящимся.
 с положительными членами. Сравним его с геометрическим рядом
с положительными членами. Сравним его с геометрическим рядом  который сходится
который сходится 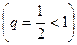 .
.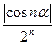
 каждый член полученного ряда не превосходит соответствующие члены геометрического ряда, ряд с положительными членами сходится, а заданный знакопеременный ряд сходится условно.
каждый член полученного ряда не превосходит соответствующие члены геометрического ряда, ряд с положительными членами сходится, а заданный знакопеременный ряд сходится условно.

 и
и 
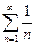 - гармонический, он расходится.
- гармонический, он расходится. сходится и вычислить приближенное значение его суммы с точностью до
сходится и вычислить приближенное значение его суммы с точностью до 
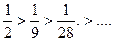 и
и