Відстань від точки до прямої
 і пряму і пряму  . Візьмемо довільну точку прямої . Візьмемо довільну точку прямої  – –  (рис.3.12). Тоді, площа паралелограма (рис.3.12). Тоді, площа паралелограма  : :
Рисунок 3.12 Приклад 1. Знайти відстань від т. Розв’язання. Знайдемо координати вектора
Підставивши дані в (3.15), отримаємо: Відповідь:
Криві другого порядку Означення 1. Криві, загальне рівняння яких має вигляд де Коло Означення 2. Крива другого порядку (3.16) є колом (рис.3.13) тоді і тільки тоді, коли: 1)
 ; ;
2) відсутній член, що містить добуток змінних координат
де Якщо Рисунок 3.13 початком координат: Еліпс Означення 3. Крива другого порядку (3.16) називається еліпсом, якщо коефіцієнти
 (3.19) (3.19)
Якщо
Рисунок 3.14 Означення 4. Точки Означення 5. Відношення Характеристична властивість еліпса Теорема 1. Для будь-якої точки еліпса сума її фокальних радіусів стала і дорівнює Доведення.
Аналогічно Оскільки
|








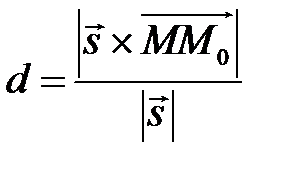 (3.15)
(3.15)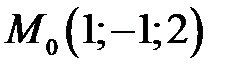 до прямої
до прямої  .
. , де
, де  :
:  . Напрямний вектор прямої
. Напрямний вектор прямої 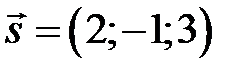 ,
,  . Тоді векторний добуток векторів
. Тоді векторний добуток векторів  дорівнює:
дорівнює:

 .
. , (3.16)
, (3.16) , називаються кривими другого порядку.
, називаються кривими другого порядку.




 , тобто
, тобто
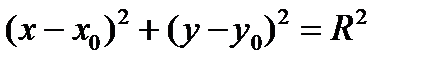 , (3.17)
, (3.17) – центр кола,
– центр кола,  – радіус кола.
– радіус кола.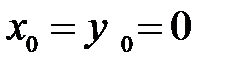 – центр кола співпадає з
– центр кола співпадає з (3.18)
(3.18)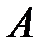 і
і  мають однакові знаки, тобто
мають однакові знаки, тобто  >
>  :
:
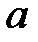








 – центр еліпса,
– центр еліпса,  – півосі еліпса.
– півосі еліпса. , то центр еліпса знаходиться в точці
, то центр еліпса знаходиться в точці  (рис.3.14) і:
(рис.3.14) і: (3.20)
(3.20) і
і 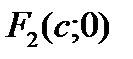 , де
, де  ,
,  >
> 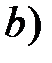 називаються фокусами еліпса.
називаються фокусами еліпса. ,
,  називається ексцентриситетом еліпса.
називається ексцентриситетом еліпса. :
:  .
.
 ,
,  .
.
 .
. .
. , то
, то  і
і 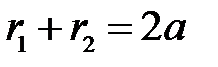 . Теорему доведено.
. Теорему доведено.


