Означення 3. Поверхня, яка складається з усіх прямих, що перетинають дану лінію  і проходять через дану т.
і проходять через дану т.  називається конічною.
називається конічною.
 Конус
Конус  – еліптичний.
– еліптичний.
 – круговий.
– круговий.
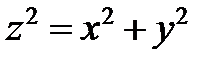
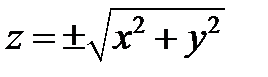
Поверхні обертання
Еліпсоїд: 
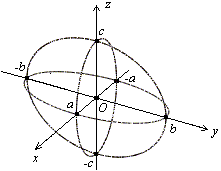
Гіперболоїди:
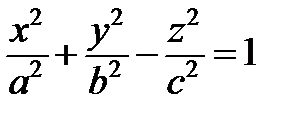

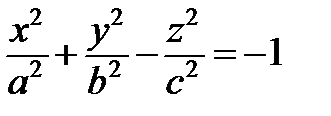
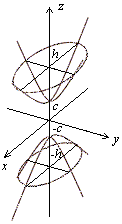
Параболоїд: 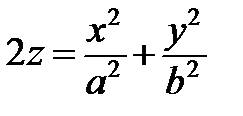
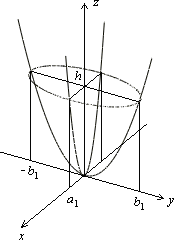
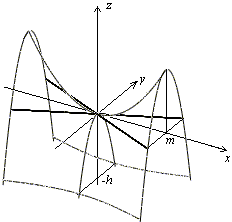
Гіперболічний параболоїд:
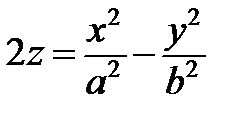
Приклад 1. Сегментна арка має форму дуги кола (рис.3.20). Скласти рівняння цього кола, знайти його центр та радіус, якщо проліт арки
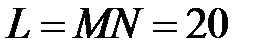
, а її підйом, тобто відношення її висоти до прольоту,
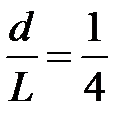
.
Рисунок 3.20 Розв’язання.
За умовою  ,
, 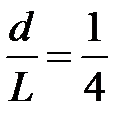 . Відповідно
. Відповідно  . В обраній системі координат точки
. В обраній системі координат точки  мають відповідно координати
мають відповідно координати  ,
, 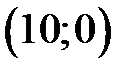 ,
,  . Оскільки арка симетрична відносно осі
. Оскільки арка симетрична відносно осі  , центр шуканого кола лежить на
, центр шуканого кола лежить на  . Запишемо рівняння кола:
. Запишемо рівняння кола: 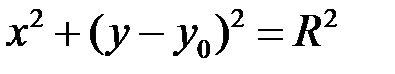 .
.
З умови, що коло проходить через точки  і
і  , складемо систему:
, складемо систему:  . Розв’язавши її, отримаємо
. Розв’язавши її, отримаємо 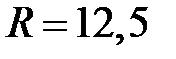 ,
,  .
.
Таким чином, центром кола є точка  , а його радіус
, а його радіус 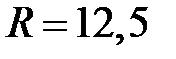 .
.
Рівняння шуканого кола:  .
.
Приклад 2. Кривошип
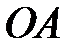
обертається з постійною кутовою швидкістю
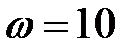
град/с та приводить в рух повзун

за допомогою шатуна
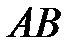
, причому
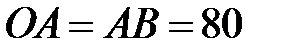
см. (рис.3.21). Скласти
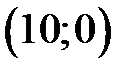
середньої точки
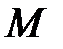
шатуна та зобразити її.
Розв’язання.
Скориставшись рисунком знаходимо:  З
З  :
:
Рисунок 3.21  .
.  . Тоді:
. Тоді:  ;
;  .
.
Оскільки кутова швидкість кривошипу 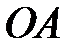 стала, то
стала, то  ,
,
 , де
, де  – час. Отримані рівняння є параметричними рівняннями траєкторії т.
– час. Отримані рівняння є параметричними рівняннями траєкторії т.  . Виключивши параметр
. Виключивши параметр  , отримаємо канонічне рівняння траєкторії:
, отримаємо канонічне рівняння траєкторії:  . Це еліпс з півосями
. Це еліпс з півосями  і
і  , зображений на (рис.3.21).
, зображений на (рис.3.21).
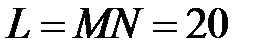 , а її підйом, тобто відношення її висоти до прольоту,
, а її підйом, тобто відношення її висоти до прольоту, 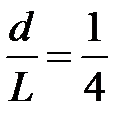 .
.
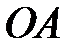 обертається з постійною кутовою швидкістю
обертається з постійною кутовою швидкістю 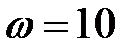 град/с та приводить в рух повзун
град/с та приводить в рух повзун  за допомогою шатуна
за допомогою шатуна 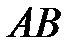 , причому
, причому 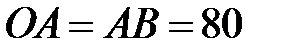 см. (рис.3.21). Скласти
см. (рис.3.21). Скласти 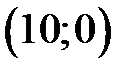 середньої точки
середньої точки 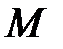 шатуна та зобразити її.
шатуна та зобразити її.

 і проходять через дану т.
і проходять через дану т.  називається конічною.
називається конічною. Конус
Конус  – еліптичний.
– еліптичний. – круговий.
– круговий.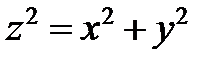
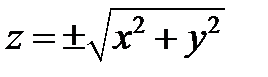


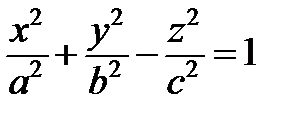

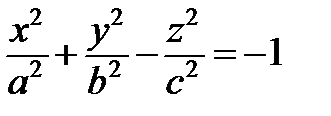

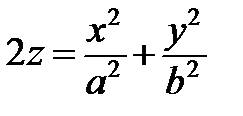

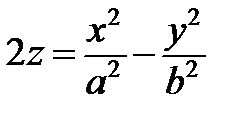





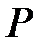

 ,
,  . В обраній системі координат точки
. В обраній системі координат точки  мають відповідно координати
мають відповідно координати  ,
,  . Оскільки арка симетрична відносно осі
. Оскільки арка симетрична відносно осі  , центр шуканого кола лежить на
, центр шуканого кола лежить на 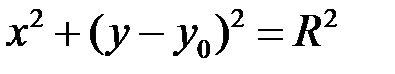 .
. і
і  , складемо систему:
, складемо систему:  . Розв’язавши її, отримаємо
. Розв’язавши її, отримаємо 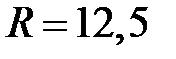 ,
,  .
. , а його радіус
, а його радіус  .
.


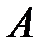


 З
З  :
: .
.  . Тоді:
. Тоді:  ;
;  .
. ,
, , де
, де  – час. Отримані рівняння є параметричними рівняннями траєкторії т.
– час. Отримані рівняння є параметричними рівняннями траєкторії т.  . Виключивши параметр
. Виключивши параметр  . Це еліпс з півосями
. Це еліпс з півосями  і
і  , зображений на (рис.3.21).
, зображений на (рис.3.21).


