1. Сума двох нескінченно малих послідовностей є нескінченно мала послідовність.
Доведення.
Нехай 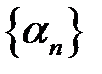 і
і 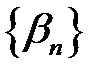 – нескінченно малі послідовності. Доведемо, що послідовність
– нескінченно малі послідовності. Доведемо, що послідовність 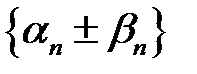 – нескінченно мала.
– нескінченно мала.
Нехай 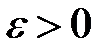 – нескінченно мала.
– нескінченно мала. 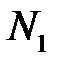 – номер, починаючи з якою
– номер, починаючи з якою 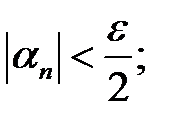
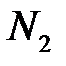 – номер, починаючи з якого
– номер, починаючи з якого 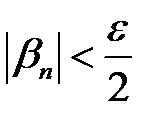 (за означенням 1). Візьмемо
(за означенням 1). Візьмемо 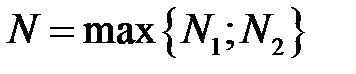 . Тоді при
. Тоді при 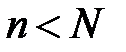 будуть одночасно виконуватись нерівності:
будуть одночасно виконуватись нерівності:
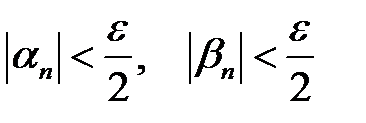
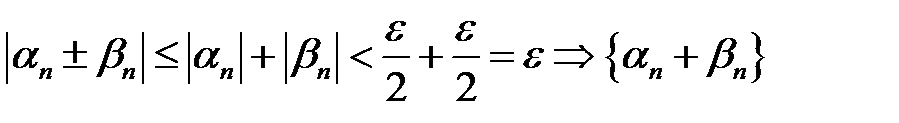 – нескінченно мала.
– нескінченно мала.
2. Добуток двох нескінченно малих послідовностей на обмежену послідовність є нескінченно мала послідовність.
Доведення.
Нехай 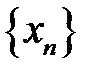 – обмежена послідовність,
– обмежена послідовність, 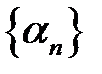 – нескінченно мала послідовність. Доведемо що
– нескінченно мала послідовність. Доведемо що 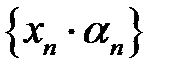 – нескінченно мала.
– нескінченно мала.
З обмеженості 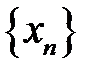 випливає, що вона обмежена
випливає, що вона обмежена 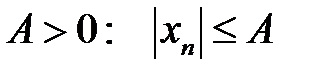 . Візьмемо
. Візьмемо 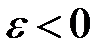 . Так як
. Так як 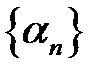 – нескінченно мала, то для
– нескінченно мала, то для 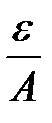 знайдеться номер
знайдеться номер 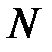 такий, що при
такий, що при 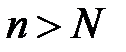 виконується нерівність
виконується нерівність 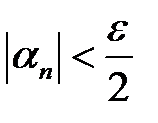 . Тоді при
. Тоді при 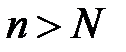 маємо:
маємо: 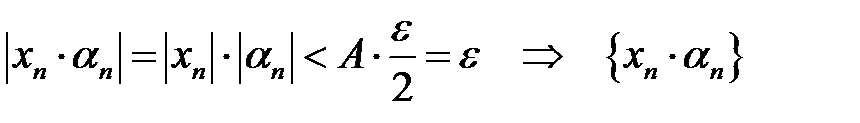 – нескінченно мала.
– нескінченно мала.
3 Добуток нескінченно малих послідовностей є нескінченно мала послідовність.
Доведення.
Нехай 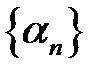 і
і 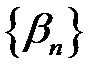 – нескінченно малі послідовності. Доведемо, що
– нескінченно малі послідовності. Доведемо, що 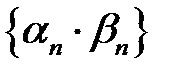 нескінченно мала послідовність.
нескінченно мала послідовність.
З того, що 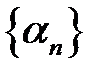 нескінченно мала, випливає, що для будь-якого
нескінченно мала, випливає, що для будь-якого 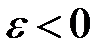 знайдеться
знайдеться 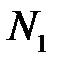 такий, що
такий, що 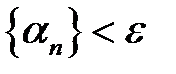 при
при 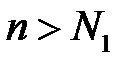 , і так як
, і так як 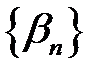 – нескінченно мала, випливає, що для
– нескінченно мала, випливає, що для 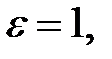 знайдеться
знайдеться 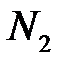 такий, що
такий, що 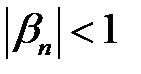 при
при 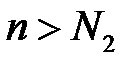 . Візьмемо
. Візьмемо 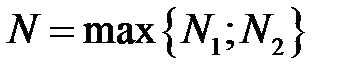 . Для
. Для 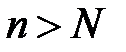 маємо:
маємо:
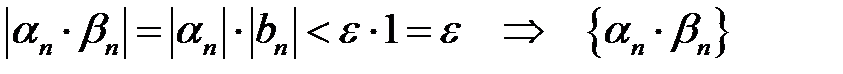 – нескінченно мала.
– нескінченно мала.
Наслідок. З трьох властивостей випливає, що сума, добуток будь-якого числа нескінченно малих послідовностей є послідовність нескінченно мала.
Теорема. Для того, щоб змінна 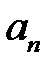 мала границю
мала границю 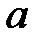 необхідно і достатньо, щоб
необхідно і достатньо, щоб 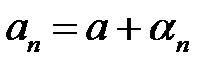 , де
, де 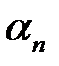 – нескінченно мала.
– нескінченно мала.
Означення 3. Послідовність 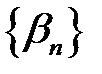 називається нескінченно великою, якщо для кожного
називається нескінченно великою, якщо для кожного 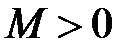 , знайдеться таке
, знайдеться таке 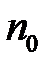 , що
, що 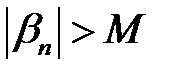 , (
, (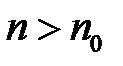 ), при цьому записують:
), при цьому записують:
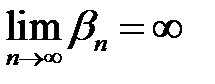 .
.

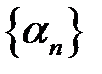 і
і 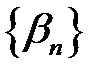 – нескінченно малі послідовності. Доведемо, що послідовність
– нескінченно малі послідовності. Доведемо, що послідовність 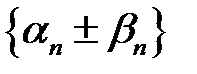 – нескінченно мала.
– нескінченно мала.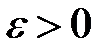 – нескінченно мала.
– нескінченно мала. 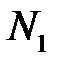 – номер, починаючи з якою
– номер, починаючи з якою 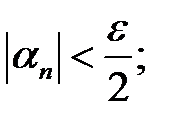
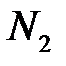 – номер, починаючи з якого
– номер, починаючи з якого 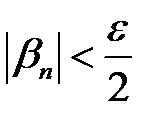 (за означенням 1). Візьмемо
(за означенням 1). Візьмемо 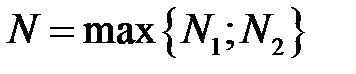 . Тоді при
. Тоді при 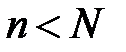 будуть одночасно виконуватись нерівності:
будуть одночасно виконуватись нерівності: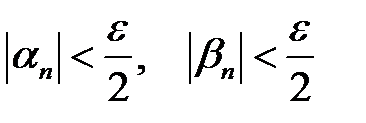
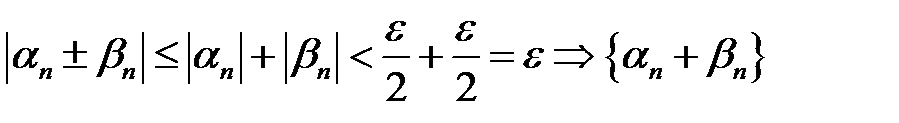 – нескінченно мала.
– нескінченно мала.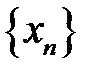 – обмежена послідовність,
– обмежена послідовність, 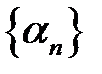 – нескінченно мала послідовність. Доведемо що
– нескінченно мала послідовність. Доведемо що 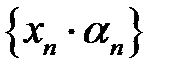 – нескінченно мала.
– нескінченно мала.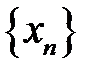 випливає, що вона обмежена
випливає, що вона обмежена 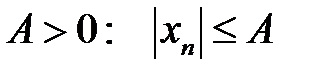 . Візьмемо
. Візьмемо 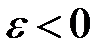 . Так як
. Так як 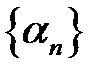 – нескінченно мала, то для
– нескінченно мала, то для 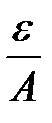 знайдеться номер
знайдеться номер 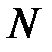 такий, що при
такий, що при 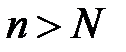 виконується нерівність
виконується нерівність 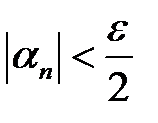 . Тоді при
. Тоді при 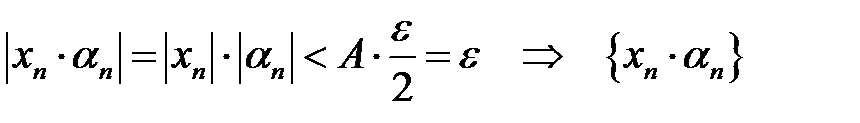 – нескінченно мала.
– нескінченно мала.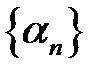 і
і 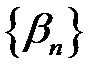 – нескінченно малі послідовності. Доведемо, що
– нескінченно малі послідовності. Доведемо, що 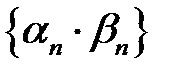 нескінченно мала послідовність.
нескінченно мала послідовність.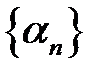 нескінченно мала, випливає, що для будь-якого
нескінченно мала, випливає, що для будь-якого 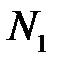 такий, що
такий, що 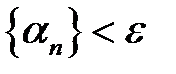 при
при 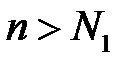 , і так як
, і так як 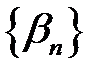 – нескінченно мала, випливає, що для
– нескінченно мала, випливає, що для 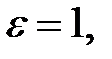 знайдеться
знайдеться 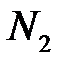 такий, що
такий, що 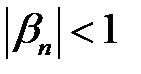 при
при 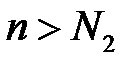 . Візьмемо
. Візьмемо 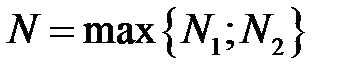 . Для
. Для 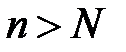 маємо:
маємо: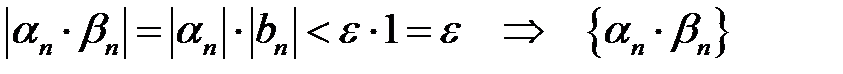 – нескінченно мала.
– нескінченно мала.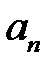 мала границю
мала границю 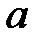 необхідно і достатньо, щоб
необхідно і достатньо, щоб 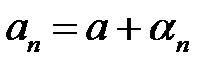 , де
, де 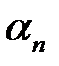 – нескінченно мала.
– нескінченно мала.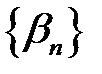 називається нескінченно великою, якщо для кожного
називається нескінченно великою, якщо для кожного 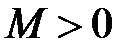 , знайдеться таке
, знайдеться таке 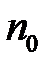 , що
, що 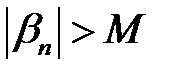 , (
, (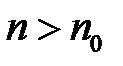 ), при цьому записують:
), при цьому записують: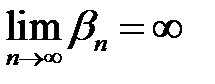 .
.


