4.1 Функція
Означення 1. Величина  – називається функцією від величини
– називається функцією від величини  , якщо за певним правилом
, якщо за певним правилом  , кожному значенню величини
, кожному значенню величини  відповідає єдине цілком визначене значення величини
відповідає єдине цілком визначене значення величини  .
.
 – називають аргументом або незалежною змінною,
– називають аргументом або незалежною змінною,  – залежною змінною.
– залежною змінною.
В даному випадку записують  ,
,  – правило за яким будь-якому
– правило за яким будь-якому  відповідає єдине значення
відповідає єдине значення  .
.
Способи задання функції
1. Аналітичний:  .
.
2. Табличний.
3. Графічний.
Означення 2. Графіком функції 
називається множина всіх точок

площини

, координати яких зв’язані даною функціональною залежністю (рис.4.1).
Рисунок 4.1
Означення 3. Якщо кожному значенню  відповідає одне значення
відповідає одне значення  , то
, то  називають однозначною функцією (
називають однозначною функцією (
 ), якщо хоча б деяким значенням
), якщо хоча б деяким значенням  відповідає декілька або нескінчена множина значень змінної
відповідає декілька або нескінчена множина значень змінної  , то
, то  називають багатозначною функцією (
називають багатозначною функцією ( ).
).
Основні елементарні функції
1. Степенева функція  (рис.4.2–4.4).
(рис.4.2–4.4).
Рисунок 4.2 Рисунок 4.3 Рисунок 4.4
2. Показникова  (рис.4.5–4.6).
(рис.4.5–4.6).
Рисунок 4.5 Рисунок 4.6
3.
Логарифмічна

(рис.4.7–4.8).
Рисунок 4.7 Рисунок 4.8
4. Тригонометричні:
1.  (рис.4.9)
(рис.4.9)
Рисунок 4.9
2.  (рис.4.10)
(рис.4.10)
Рисунок 4.10
3.  (рис.4.11)
(рис.4.11)
Рисунок 4.11
4.  (рис.4.12)
(рис.4.12)
Рисунок 4.12
Взаємообернені функції
Нехай дано функцію 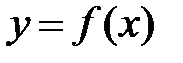 ,
,  ,
,  , тоді
, тоді  або
або  буде взаємооберненою відносно
буде взаємооберненою відносно 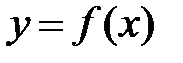 . Графіки взаємообернених функцій симетричні відносно прямої
. Графіки взаємообернених функцій симетричні відносно прямої  (бісектриси першого і третього координатних кутів) (рис.4.13).
(бісектриси першого і третього координатних кутів) (рис.4.13).
Рисунок 4.13
 називається множина всіх точок
називається множина всіх точок  площини
площини  , координати яких зв’язані даною функціональною залежністю (рис.4.1).
, координати яких зв’язані даною функціональною залежністю (рис.4.1).
 (рис.4.7–4.8).
(рис.4.7–4.8).

 – називається функцією від величини
– називається функцією від величини  , якщо за певним правилом
, якщо за певним правилом  , кожному значенню величини
, кожному значенню величини 



 ), якщо хоча б деяким значенням
), якщо хоча б деяким значенням  ).
). (рис.4.2–4.4).
(рис.4.2–4.4).











 (рис.4.5–4.6).
(рис.4.5–4.6).















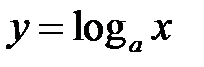





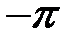


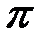




 (рис.4.9)
(рис.4.9)


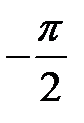


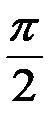
 (рис.4.10)
(рис.4.10)




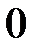



 (рис.4.11)
(рис.4.11)






 (рис.4.12)
(рис.4.12)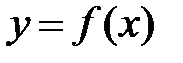 ,
,  ,
,  , тоді
, тоді  або
або  буде взаємооберненою відносно
буде взаємооберненою відносно  (бісектриси першого і третього координатних кутів) (рис.4.13).
(бісектриси першого і третього координатних кутів) (рис.4.13).






