Рівняння кривих другого порядку в полярній системі координат
1) 2) Деякі криві другого, третього порядку
Кардіоїда
Циклоїда
Архімедова спіраль
Лемніската Бернуллі
Декартів лист
Астроїда
Троянди
Параметричне задання рівняння лінії
Наприклад в механіці т. Розглянемо параметричне рівняння кола, коло В трикутнику Рисунок 3.18 Рівняння кола в полярній системі координат: Рівняння еліпса в полярній системі координат: Приклад 1. Побудувати криву
Приклад 2. Побудувати криву Розв’язання.
Поверхні другого порядку Сфера
де При
Рисунок 3.19 Циліндричні поверхні Означення 2. Поверхня, що складається з усіх прямих, що перетинають дану лінію
Еліптичний циліндр:
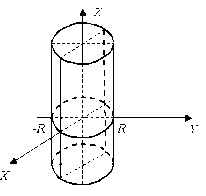
Круговий циліндр:
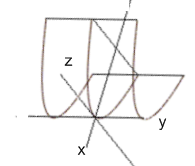
Параболічний циліндр:
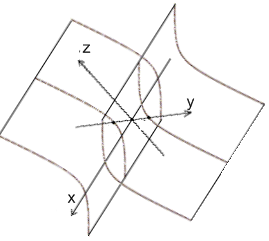
Гіперболічний циліндр:
|
– коло.
– еліпс.
Інколи замість рівнянь ліній, які пов’язують прямокутні координати 
та 
, розглядають параметричні рівняння, які визначають зміну величини 
(параметра).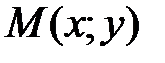
є функція від часу 
: 
(рис.3.18).
: 
, 
.
. 
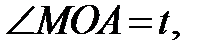
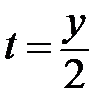– парабола.
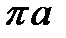
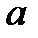
Означення 1. Сферою радіуса 
називається множина всіх точок простору, відстань від кожної точки якої до даної точки (центру) дорівнює 
(рис.3.19).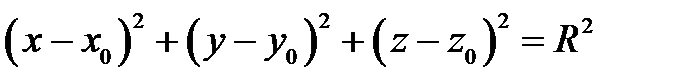
,
– центр сфери.
.
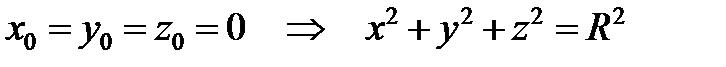називається циліндричною поверхнею.
