Властивості скалярного добутку
1. 2. 3. 4. 5. 6. 7. Зауваження:
2.10 Векторний добуток векторів
Рисунок 2.13 Означення 2. Векторним добутком вектора 1) вектор 2) вектори 3) Позначають: Геометричний зміст: векторний добуток Зауваження. Із означення 2 випливає те, що для колінеарності двох ненульових векторів необхідно і достатньо, щоб їхній векторний добуток дорівнював нулю.
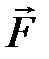 діє на точку діє на точку 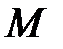 , то момент цієї сили , то момент цієї сили 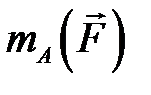 відносно т. відносно т. 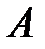 дорівнює векторному добутку векторів дорівнює векторному добутку векторів 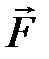 і і 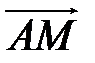 : : 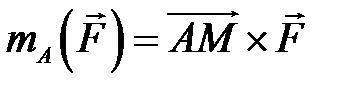 (рис.2.14). Момент відносно початку координат т. (рис.2.14). Момент відносно початку координат т.  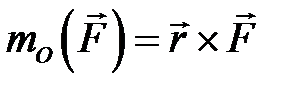 , , 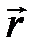 – радіус-вектор т. – радіус-вектор т. 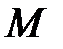 . .
Рисунок 2.14 Також за допомогою векторного добутку знаходиться швидкість точки твердого тіла, що обертається навколо нерухомої осі, тобто:
|

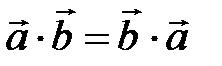 .
. .
. .
.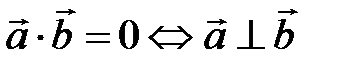 при
при  .
. .
.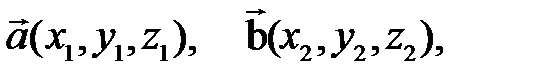 то
то 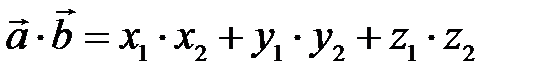 .
.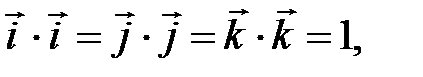
 .
.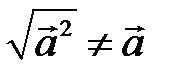 , а
, а 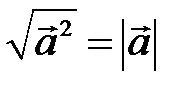 .
.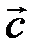
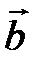
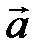
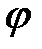
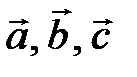 – права,
– права, 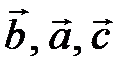 – ліва (рис.2.13).
– ліва (рис.2.13).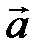 на
на 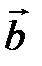 називається вектор
називається вектор  , який задовольняє наступні умови:
, який задовольняє наступні умови: до
до  і
і 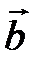 ;
;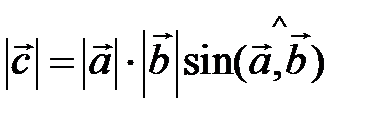 .
. або
або 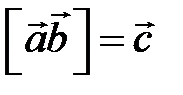 .
.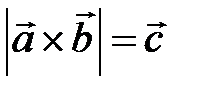 .
.
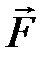
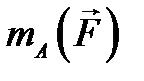
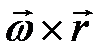 , де
, де 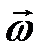 – вектор кутової швидкості,
– вектор кутової швидкості, 


