Метод Жордана-Гауса
Метод ґрунтується на елементарних перетвореннях системи лінійних рівнянь: а) рівняння системи можна множити на число відмінне від нуля і додавати до будь-якого іншого рівняння; б) рівняння системи можна міняти місцями. Приклад 2. Розв’язати систему лінійних рівнянь методом Жордана-Гауса: Розв’язання. Запишемо розширену матрицю системи та перетворимо її. 1. На місці елемента 2. У випадку коли пункт 1 виконати не можливо, ділимо елементи 1-го рядка на 3. Записуємо матрицю, перетворюючи її елементи: 1-й стовпчик занулюємо і зберігаємо елементи рядка, в якому міститься головний елемент, інші перераховуємо за правилом чотирикутника (як визначник другого порядку, але завжди починаючи з головного елемента). Для прикладу, на місці елемента Після перетворення за Аналогічно утворюємо 1 на місці елемента Таким чином, в стовпчику вільних коефіцієнтів отримуємо значення
Відповідь:
|


 має бути 1. Він вважається головним. Його можна отримати, якщо поміняти місцями рядки або стовпці системи, при цьому потрібно зафіксувати місце змінних
має бути 1. Він вважається головним. Його можна отримати, якщо поміняти місцями рядки або стовпці системи, при цьому потрібно зафіксувати місце змінних  . У даному прикладі поміняємо місцями перший та другий стовпці матриці системи. Отже, на першому місці знаходитиметься
. У даному прикладі поміняємо місцями перший та другий стовпці матриці системи. Отже, на першому місці знаходитиметься  , на другому –
, на другому – 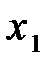 , на третьому –
, на третьому –  .
. замість “
замість “  ” запишемо “
” запишемо “  ”, оскільки,
”, оскільки, 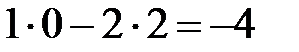 і т.д.
і т.д. , але елементи 1-го стовпця залишаємо незмінними до кінця перетворення. Після отримання 1 на місці
, але елементи 1-го стовпця залишаємо незмінними до кінця перетворення. Після отримання 1 на місці  .
. .
. .
.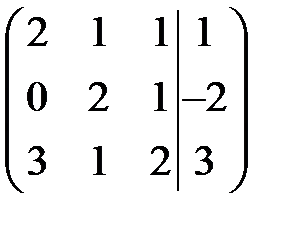






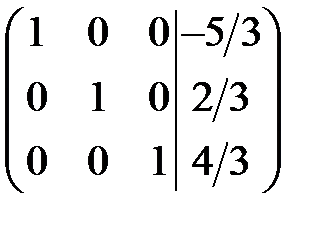 .
. ;
;  ;
;  .
.


