Обернена матрицяОзначення 1. Оберненою матрицею Означення 2. Виродженою називається матриця, визначник якої дорівнює нулю. Якщо визначник матриці не дорівнює нулю, то матриця називається невиродженою. Теорема 1. (Існування та обчислення оберненої матриці). Якщо матриця Доведення. За означенням 1 маємо:
Алгоритм знаходження оберненої матриці.
Приклад 1. Дано Розв’язання. Перевіримо чи матриця невироджена: Обчислимо алгебраїчні доповнення елементів матриці:
Відповідь: Невироджені системи лінійних рівнянь Означення 1. Система називається невиродженою, якщо визначник матриці Означення 2. Матриця Означення 3. Матриця, складена з елементів матриці системи та стовпчика вільних коефіцієнтів системи, називається розширеною: Систему (1.1) можна записати в матричному вигляді
Методи розв'язування невироджених систем лінійних рівнянь
|
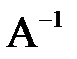до матриці 
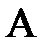називається матриця того ж порядку, яка задовольняє умові 
, де 
– одинична матриця того ж порядку що й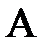 
.
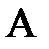
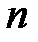-го порядку невироджена, тобто 
, то існує обернена до неї матриця: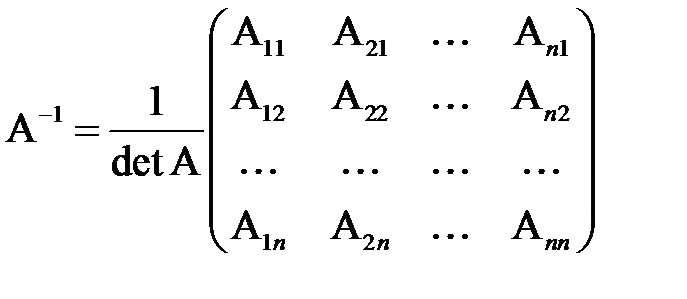 
.
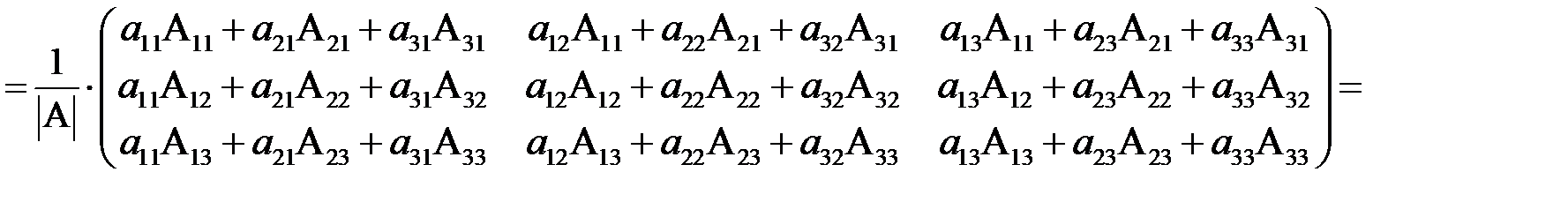
. Теорему доведено.
. Знайти 
.
= 
= 
.
.
.
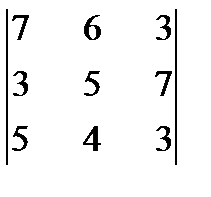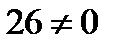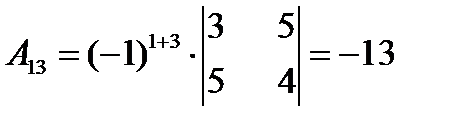
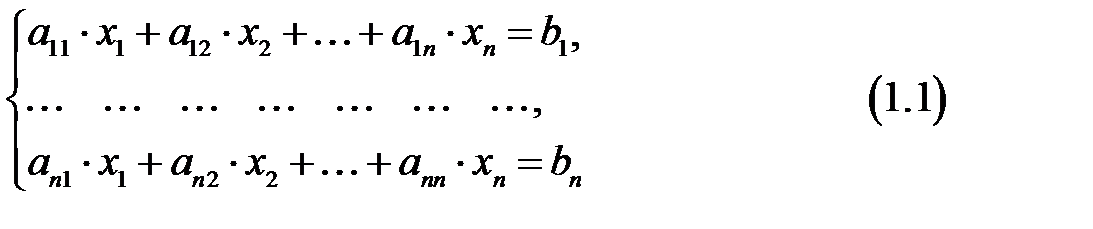
відмінний від нуля 
.
, складена з коефіцієнтів при невідомих, називається матрицею системи.
.
, де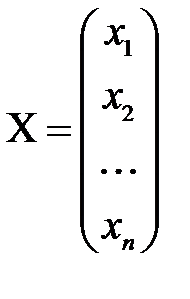
, 
.
