Правила обчислення визначників третього порядку1. Правило трикутника (Саррюса). 2. Правило розкладу за елементами рядка (стовпця) теорема 1. 3. Метод занулення. Приклад3. Обчислити визначник методом занулення Розв’язання. Накопичуємо “0” в Отримаємо: Розкладемо визначник за елементами 1-го стовпця:
1.4 Визначники матриць n-гo порядку (n Означення 1. Визначником матриці п-го порядку називається сума добутків елементів Зауваження: 1. Всі властивості визначників другого порядку справедливі і для визначників 2. Визначники 3. Правило трикутника справедливе тільки для визначників третього порядку. Приклад 1. Обчислити визначник Розв’язання. Виберемо для перетворення другий рядок. Накопичуємо “0” в 1) елементи 2-горядка помножимо на “ 2) елементи 2-го рядка множимо на “ 3) елементи 2-го рядка множимо на “ 4-го рядка. Отримаємо: Розкладемо визначник за елементами 1-го стовпця:
Маємо визначник 3-го порядку. Обчислимо його за правилом трикутника:
|
.
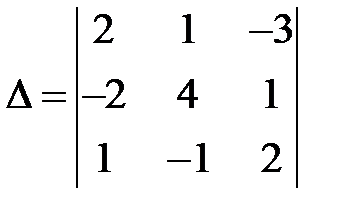-му стовпці: елементи 3-горядка помножимо на “ 
” і додамо до елементів 1-го рядка; елементи 3-го рядка помножимо на “ 
” і додамо до елементів 2-го рядка.
.
.
4)
-го рядка на їх алгебраїчні доповнення.
-го порядку.
.
” і додамо до елементів 1-го рядка;
” і додамо до елементів 3-го рядка;
” і додамо до елементів
.
.
.
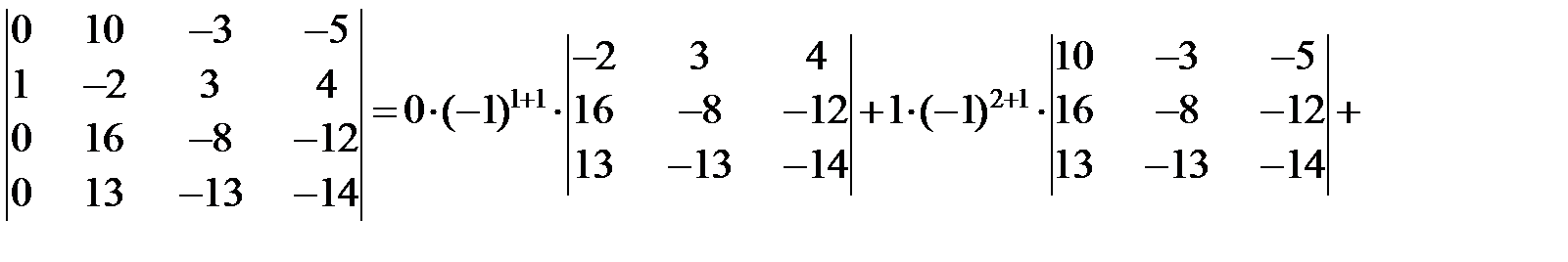
