Множення вектора на число
 на число на число 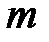 називається вектор називається вектор 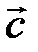 , який задовольняє наступні умови: , який задовольняє наступні умови:
1) довжина вектора модуль числа 2) якщо якщо
Рисунок 2.5 Властивості добутку вектора на число 1. 2. 3. 4. 2.3 Орт вектора. Умова колінеарності Означення 1. Вектор, модуль якого дорівнює одиниці, називається ортом (одиничним вектором). Означення 2. Ортом ненульового вектора Справедлива рівність: Теорема 1. (Ознака колінеарності 2-х векторів) Для того, щоб два вектори були колінеарні необхідно і достатньо, щоб один із них дорівнював добутку деякого числа на інший вектор.
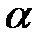 , , 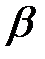 , , 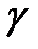 . Напрямними косинусами осі . Напрямними косинусами осі  (або напрямку (або напрямку  ) називаються косинуси цих кутів ( ) називаються косинуси цих кутів (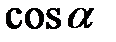 , , 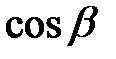 , , 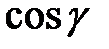 ). Якщо напрямок заданий одиничним вектором ). Якщо напрямок заданий одиничним вектором  , то напрямні косинуси є його координатами , то напрямні косинуси є його координатами 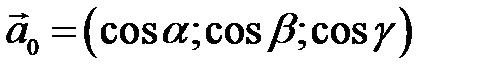 . Напрямні косинуси пов’язані між собою . Напрямні косинуси пов’язані між собою
Рисунок 2.6 співвідношенням:
2.4 Лінійна залежність та незалежність векторів Означення 1. Вектори Якщо вектори Таким чином, якщо вектори лінійно залежні, то хоча б один із них лінійно виражається через решту векторів. Геометрично:
.
Рисунок 2.7 Теорема 1. (Про лінійну залежність 2-х векторів) Два вектори лінійно залежні тоді і тільки тоді, коли вони колінеарні. Доведення.
Тоді за ознакою колінеарності Теорему доведено. Теорема 2. (Про лінійну залежність 3-х векторів) Три вектори Доведення. 1. Необхідність. Нехай а) якщо б) якщо 2. Достатність. Нехай а) б)
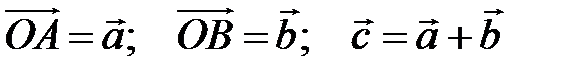 ; ;
2)
Рисунок 2.8 Наслідок: 1. Три компланарні вектори лінійно незалежні. 2. Чотири вектори в трьохвимірному лінійному просторі лінійно залежні завжди. Теорема 3. Якщо два вектори Доведення.
Розглянемо два випадки: а) нехай, наприклад, б) Так як
Теорему доведено. Теорема 4. Якщо три вектори
2.5 Базис і координати вектора Означення 1. Множину найрізноманітніших систем ( Кожну таку систему чисел назвемо точкою або вектором Rn. Числа Означення 2. Сукупність Зауваження. Простір називається лінійним векторним простором, якщо в ньому визначені операції додавання векторів і множення на число. Теорема 1. Кожен вектор Числа
|



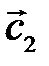
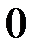 , то
, то  співнапрямлені,
співнапрямлені, ,
,  .
.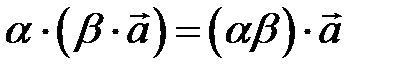 .
. .
. .
. , модуль якого дорівнює одиниці, а напрямок співпадає з напрямком вектора
, модуль якого дорівнює одиниці, а напрямок співпадає з напрямком вектора  .
. ,
, 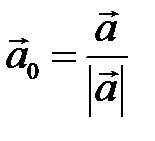 .
.

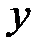




 .
. ,
,  …
…  називаються лінійно залежними, якщо існують такі числа
називаються лінійно залежними, якщо існують такі числа  одночасно не всі рівні нулю, що виконується рівність
одночасно не всі рівні нулю, що виконується рівність  . В іншому випадку вектори називаються лінійно незалежними.
. В іншому випадку вектори називаються лінійно незалежними. , тоді
, тоді 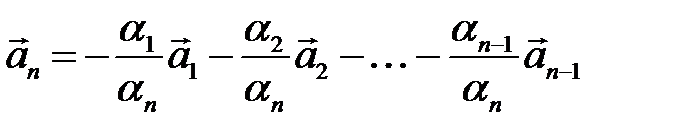 тобто,
тобто,  .
. (рис. 2.7).
(рис. 2.7).




 – лінійно залежні
– лінійно залежні 
 .
. .
.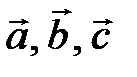 лінійно залежні тоді і тільки тоді, коли вони компланарні.
лінійно залежні тоді і тільки тоді, коли вони компланарні. :
: , то
, то  лежить з ними на одній прямій, тоді
лежить з ними на одній прямій, тоді  , тоді за правилом паралелограма маємо, що всі вектори лежать в одній площині
, тоді за правилом паралелограма маємо, що всі вектори лежать в одній площині  компланарні.
компланарні.

 (рис.2.8).
(рис.2.8).





 тоді
тоді 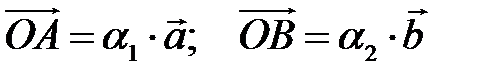

 що лежить в площині векторів
що лежить в площині векторів  і
і  єдиним способом.
єдиним способом. одночасно не рівні нулю, що
одночасно не рівні нулю, що  .
. , тоді
, тоді 

 – лінійно залежні:
– лінійно залежні: 
 .
. ,
,  , або
, або  .
. .
.
 або
або 
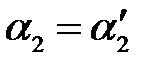
 .
. можна лінійно виразити через
можна лінійно виразити через  .
. ) дійсних чисел називають n-вимірним дійсним простором і позначають через Rn.
) дійсних чисел називають n-вимірним дійсним простором і позначають через Rn. лінійно незалежних векторів
лінійно незалежних векторів  -вимірного простору називається його базисом.
-вимірного простору називається його базисом. лінійного
лінійного  -вимірного простору можна представити єдиним способом у вигляді лінійної комбінації векторів базису
-вимірного простору можна представити єдиним способом у вигляді лінійної комбінації векторів базису 
 в базисі
в базисі  , тобто
, тобто  .
.


