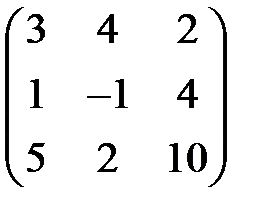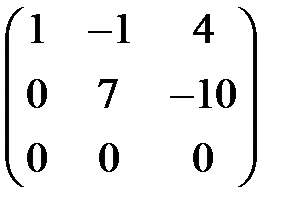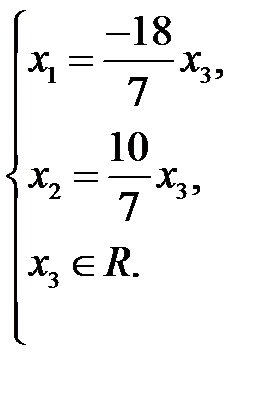Довільні системи лінійних рівнянь
Розглянемо прямокутну матрицю Означення 1. Рангом матриці Якщо всі елементи матриці дорівнюють нулю, то ранг такої матриці також дорівнює нулю. Означення 2. Будь-який, відмінний від нуля мінор матриці, порядок якого дорівнює рангу цієї матриці називається базисним мінором матриці. Ранг матриці позначимо через Елементарні перетворення не змінюють ранг матриці: 1. Заміна рядків стовпцями і навпаки. 2. Перестановка рядків матриці. 3. Закреслення рядка матриці, всі елементи якого дорівнюють нулю. 4. Множення будь-якого рядка на число відмінне від нуля і додавання його до іншого рядка. Означення 3. Якщо в матриці будь-який рядок може бути представлений у вигляді суми інших паралельних йому рядків, помножених відповідно на числа Означення 4. L – паралельних рядків матриці називаються лінійно залежними, якщо хоча б один з них є лінійною комбінацією решти. В протилежному випадку вони лінійно незалежні. Теорема 1. (Про базисний мінор) 1. Будь-який рядок (стовпчик) матриці є лінійною комбінацією базисних рядків. 2. Базисні рядки матриці лінійно незалежні. При обчисленні рангу матриці використовуються елементарні перетворення, метод зведення матриці до трапецієвидної форми та інші. Приклад 1. Знайти ранги наступних матриць: 1. Ранг матриці дорівнює кількості ненульових рядків: 2.
Теорема 2. (Кронекера-Капеллі) Для сумісності системи
необхідно і достатньо, щоб ранг матриці системи дорівнював рангу її розширеної матриці. Доведення. 1. Необхідність. Нехай система (1.2) сумісна і
Виконаємо над матрицею
Ранг не зміниться 2. Достатність. Нехай матриці
Тоді перші
Можливі два випадки: 1) 2) Приклад 2. Довести сумісність та знайти розв’язок системи лінійних рівнянь: Розв’язання. Запишемо розширену матрицю даної системи:
Зробимо нижче головної діагоналі нулі:
Маємо систему: Виразимо Відповідь: Приклад 3. Дослідити на сумісність систему: Розв’язання. Запишемо розширену матрицю системи і зведемо її до трапецієвидної форми:
Відповідь: Система несумісна.
1.8 Однорідні системи лінійних рівнянь Розглянемо систему рівнянь:
Цю систему назвемо однорідною. Вона завжди сумісна, так як Теорема 1. Для того, щоб система (1.5) мала ненульовий розв’язок необхідно і достатньо щоб ранг Доведення. Дійсно, якщо Теорема 2. Для того, щоб однорідна система Доведення. Умова Приклад 1. Розв’язати систему: Розв’язання.
Відповідь: Приклад 2. Розв’язати систему: Розв’язання.
Відповідь:
|

 .
. називається найбільший порядок мінору цієї матриці, відмінного від нуля.
називається найбільший порядок мінору цієї матриці, відмінного від нуля. . Якщо
. Якщо  , то матриці
, то матриці  називаються еквівалентними
називаються еквівалентними  .
. ,
,  ,…,
,…,  , то кажуть, що даний рядок є лінійною комбінацією вказаних рядків.
, то кажуть, що даний рядок є лінійною комбінацією вказаних рядків.



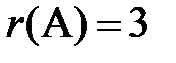 .
.
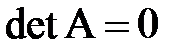


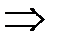
 .
.
 ,
,  ,…,
,…,  – один із її розв’язків. Покажемо, що
– один із її розв’язків. Покажемо, що  , де
, де 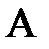 – матриця системи,
– матриця системи,  – розширена матриця системи. Підставимо
– розширена матриця системи. Підставимо 
 ), другий на (
), другий на ( ),...,
),...,  -ий на (
-ий на ( ). Тоді, враховуючи (1.3), отримаємо:
). Тоді, враховуючи (1.3), отримаємо: .
. .
. і
і  . Покажемо, що система (1.2) сумісна. Можна припустити, що відмінний від нуля визначник
. Покажемо, що система (1.2) сумісна. Можна припустити, що відмінний від нуля визначник  порядку
порядку 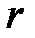 знаходиться в лівому верхньому кутку, як матриці
знаходиться в лівому верхньому кутку, як матриці  .
. рядків системи є наслідками
рядків системи є наслідками  Теорема доведена.
Теорема доведена. , тобто число рівнянь системи дорівнюють числу невідомих, причому визначник
, тобто число рівнянь системи дорівнюють числу невідомих, причому визначник  цієї системи
цієї системи  . Система має єдиний розв'язок, який знаходиться за формулами Крамера, матричним методом чи методом Жордана-Гауса.
. Система має єдиний розв'язок, який знаходиться за формулами Крамера, матричним методом чи методом Жордана-Гауса. <
<  , тобто число рівнянь системи менше числа невідомих, тоді система має безліч розв’язків.
, тобто число рівнянь системи менше числа невідомих, тоді система має безліч розв’язків.
 .
. .
.
 і
і  через
через  і
і  :
: 





 .
. .
.
 , і має тривіальний розв’язок
, і має тривіальний розв’язок  .
.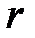 її матриці був менший за
її матриці був менший за  .
.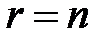 , то система має один розв’язок – тривіальний. Якщо
, то система має один розв’язок – тривіальний. Якщо  <
<  , то (1.5) є невизначеною системою, тобто має безліч розв’язків, в тому числі і безліч ненульових розв’язків.
, то (1.5) є невизначеною системою, тобто має безліч розв’язків, в тому числі і безліч ненульових розв’язків. лінійних рівнянь з
лінійних рівнянь з  невідомими мала ненульовий розв’язок, необхідно і достатньо, щоб її визначник
невідомими мала ненульовий розв’язок, необхідно і достатньо, щоб її визначник  .
.

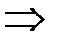
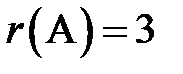 .
. .
.
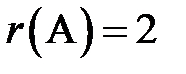 ,
,  ,
,